题目内容
 如图,点A为双曲线y=-
如图,点A为双曲线y=-| 2 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:设B(a,a),则A(-
,a).所以利用两点间的距离公式可以求得线段AB、OA的长度;然后可以AB2-OA2的值.
| 2 |
| a |
解答:解:∵直线AB平行于x轴交直线y=x于点A,
故设B(a,a),
∵A为双曲线y=-
(x<0)上一点,
∴A(-
,a),
∴AB=a+
,OA=
,
∴AB2-OA2=(a+
)2-[a2+(
)2]=4.
故设B(a,a),
∵A为双曲线y=-
| 2 |
| x |
∴A(-
| 2 |
| a |
∴AB=a+
| 2 |
| a |
a2+(
|
∴AB2-OA2=(a+
| 2 |
| a |
| 2 |
| a |
点评:本题考查了反比例函数与一次函数图象上点的坐标特征,勾股定理的应用,利用点B的横坐标表示出点A的坐标是解题的关键.

练习册系列答案
相关题目
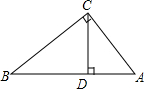 如图,已知Rt△ABC中,∠C=90°,CD⊥AB于D,利用三角函数知识证明:
如图,已知Rt△ABC中,∠C=90°,CD⊥AB于D,利用三角函数知识证明: 如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.
如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.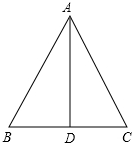 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,BD=2cm,求BC的长和∠ADC的大小.
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,BD=2cm,求BC的长和∠ADC的大小.