题目内容
已知有理数x,y,z满足(x-4)2+
|x+y-z|=0,则(5x+3y-3z)2008的末尾数字是 .
| 1 |
| 4 |
考点:尾数特征,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:首先根据非负数的性质求得x的值和y-z的数值,代入代数式,找出规律,利用规律判定幂的末尾数字即可.
解答:解:∵(x-4)2+
|x+y-z|=0,
∴x-4=0,x+y-z=0,
∴x=4,y-z=-4,
∴(5x+3y-3z)2008=82008;
81的末位数字是8,
82的末位数字是4,
83的末位数字是2,
84的末位数字是6,
85的末位数字是8,
…
四次一循环,因为2008÷4=502;
所以82008的末位数字是6,即(5x+3y-3z)2008的末尾数字是6.
故答案为:6.
| 1 |
| 4 |
∴x-4=0,x+y-z=0,
∴x=4,y-z=-4,
∴(5x+3y-3z)2008=82008;
81的末位数字是8,
82的末位数字是4,
83的末位数字是2,
84的末位数字是6,
85的末位数字是8,
…
四次一循环,因为2008÷4=502;
所以82008的末位数字是6,即(5x+3y-3z)2008的末尾数字是6.
故答案为:6.
点评:此题考查幂的末位数字,注意从计算中找规律;同时考查了非负数的性质,代数式求值等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若式子
的值比
的值大2,则x的值为( )
| x-1 |
| 4 |
| 2-x |
| 3 |
| A、1 | B、5 | C、-5 | D、11 |
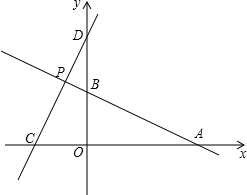 如图,直线AB:y=-
如图,直线AB:y=- 如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.
如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.