题目内容
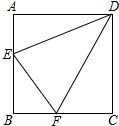 在正方形ABCD中,∠EDF=45°,求证:EF=AE+CF.
在正方形ABCD中,∠EDF=45°,求证:EF=AE+CF.考点:旋转的性质,全等三角形的判定与性质,正方形的性质
专题:证明题
分析:根据正方形的性质得DA=DC,∠A=∠ADC=90°,则可把Rt△DAE绕点D逆时针旋转90°得到Rt△DCG,如图,根据旋转的性质AE=CG,DE=DG,∠EDG=90°,∠DCG=∠A=90°,则可判断点G在BC的延长线上,所以FG=FC+CG,然后证明△DFE≌△DFG,得到EF=FG,易得EF=FC+AE.
解答:证明: ∵四边形ABCD为正方形,
∵四边形ABCD为正方形,
∴DA=DC,∠A=∠ADC=90°,
把Rt△DAE绕点D逆时针旋转90°得到Rt△DCG,如图,
∴AE=CG,DE=DG,∠EDG=90°,∠DCG=∠A=90°,
而∠DCF=90°,
∴点G在BC的延长线上,
∴FG=FC+CG,
∵∠EDF=45°,
∴∠FDG=∠EDG-∠EDF=45°,
在△DFE和△DFG中,
,
∴△DFE≌△DFG(SAS),
∴EF=FG,
∴EF=FC+CG=FC+AE.
 ∵四边形ABCD为正方形,
∵四边形ABCD为正方形,∴DA=DC,∠A=∠ADC=90°,
把Rt△DAE绕点D逆时针旋转90°得到Rt△DCG,如图,
∴AE=CG,DE=DG,∠EDG=90°,∠DCG=∠A=90°,
而∠DCF=90°,
∴点G在BC的延长线上,
∴FG=FC+CG,
∵∠EDF=45°,
∴∠FDG=∠EDG-∠EDF=45°,
在△DFE和△DFG中,
|
∴△DFE≌△DFG(SAS),
∴EF=FG,
∴EF=FC+CG=FC+AE.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和正方形的性质.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
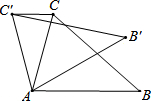 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )| A、30° | B、35° |
| C、40° | D、50° |
 如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.
如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.
 如图,已知AB是直径,弦CD与AB相交于点P,且将AB分成2和8两段,∠DPB=30°,求弦CD的长.
如图,已知AB是直径,弦CD与AB相交于点P,且将AB分成2和8两段,∠DPB=30°,求弦CD的长.