Question

14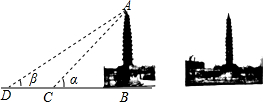．聊城流传着一首家喻户晓的民谣：“东昌府，有三宝，铁塔、古楼、玉皇皋．”被人们誉为三宝之一的铁塔，初建年代在北宋早起，是本市现存最古老的建筑．如图，测绘师在离铁塔10米处的点C测得塔顶A的仰角为α，他又在离铁塔25米处的点D测得塔顶A的仰角为β，若tanαtanβ=1，点D，C，B在同一条直线上，那么测绘师测得铁塔的高度约为（参考数据：$\sqrt{10}$≈3.162）（　　）

• A． 15.81米
• B． 16.81米
• C． 30.62米
• D． 31.62米

Answer 1

分析 先根据锐角三角函数的定义用tanα与tanβ表示出AB的长，再由tanαtanβ=1即可得出结论．

解答 解：∵BC=10米，BD=25米，
∴在Rt△ABC中，AB=BC•tanα=10tanα①，在Rt△ABD中，AB=BD•tanβ=25tanβ②．
∵tanαtanβ=1，
∴AB²=10tanα•25tanβ=250，
∴AB=$\sqrt{250}$=5$\sqrt{10}$≈5×3.162=15.81（米）．
故选A．

点评 本题考查的是解直角三角形的应用-仰角俯角问题，熟记锐角三角函数的定义是解答此题的关键．