题目内容
20.已知y+a与x-b成正比例(其中a、b都是常数).(1)试说明y是x的一次函数;
(2)如果x=-1时,y=-15;x=7时,y=1,求这个一次函数的解析式.
分析 (1)因为y+a与x+b成正比例,设比例系数为k,列等式后变形进行说明;
(2)把“x=-1时,y=-15;x=7时,y=1”分别代入一次函数解析式,列出关于系数的方程组,通过解方程求得它们的值即可.
解答 解:(1)∵y+a与x+b成正比例,
设比例系数为k,则y+a=k(x-b),
整理得:y=kx-kb-a,
∴y是x的一次函数;
(2)把x=-1时,y=-15;x=7时,y=1分别代入y=kx-kb-a,得
$\left\{\begin{array}{l}{-15=-k-kb-a}\\{1=7k-kb-a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{kb+a=13}\end{array}\right.$,
则该一次函数为:y=2x-13.
点评 本题考查了一次函数解析式的一般形式,关键是根据y+a与x-b成正比例,设比例系数为k,列等式.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
11.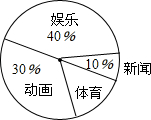 某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )
某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )
 某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )
某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )| A. | 300名 | B. | 250名 | C. | 200名 | D. | 150名 |
8.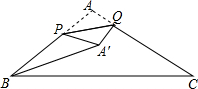 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )| A. | 2$\sqrt{3}$-2 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
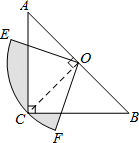 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为π-2平方单位.
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为π-2平方单位. 如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.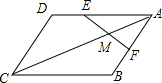 如图,AC是?ABCD的对角线,点E在AD上,AE=2DE,点F是AB的中点,连接EF交AC于点M,若AC=14,则AM=4.
如图,AC是?ABCD的对角线,点E在AD上,AE=2DE,点F是AB的中点,连接EF交AC于点M,若AC=14,则AM=4. 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)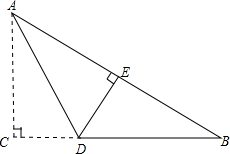 如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.
如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.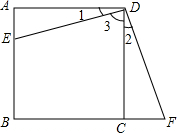 如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形.
如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形.