题目内容
19.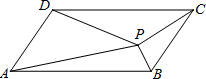 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )| A. | S1+S2=S3+S4 | B. | S1+S2>S3+S4 | C. | S1+S3=S2+S4 | D. | S1+S2<S3+S4 |
分析 由平行四边形的性质得出S1+S3=$\frac{1}{2}$平行四边形ABCD的面积,S2+S4=$\frac{1}{2}$平行四边形ABCD的面积,即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴S1+S3=$\frac{1}{2}$平行四边形ABCD的面积,
S2+S4=$\frac{1}{2}$平行四边形ABCD的面积,
∴S1+S3=S2+S4,
故选:C.
点评 此题考查了平行四边形的性质以及三角形的面积问题.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
9.下列图形选自历届世博会会徽,其中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.方程组$\left\{\begin{array}{l}{2x+y=3}\\{3x-z=7}\\{x-y+3z=0}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=1}\end{array}\right.$ |
11.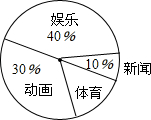 某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )
某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )
 某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )
某校为调查1000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况,随机抽取了部分学生进行调查,并利用调查数据作出如图所示的扇形统计图.根据图中信息,可以估算出该校喜爱体育节目的学生共有( )| A. | 300名 | B. | 250名 | C. | 200名 | D. | 150名 |
8.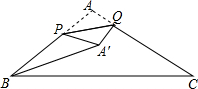 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )| A. | 2$\sqrt{3}$-2 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
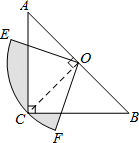 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为π-2平方单位.
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为π-2平方单位. 如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.