题目内容
8．
如图，AB∥DC，且AD∥BC，∠α=50°，求∠C的度数．
分析 首先根据两直线平行，同位角相等可得∠B=∠α=50°，再根据两直线平行，同旁内角互补可得∠B+∠C=180°，进而可得∠C的度数．
解答 解：∵AD∥BC，
∴∠B=∠α=50°，
∵AB∥DC，
∴∠B+∠C=180°，
∴∠C=180°-50°=130°．
点评 此题主要考查了平行线的性质，关键是掌握平行线性质定理
定理1：两条平行线被第三条直线所截，同位角相等． 简单说成：两直线平行，同位角相等．
定理2：两条平行线被地三条直线所截，同旁内角互补．．简单说成：两直线平行，同旁内角互补．
定理3：两条平行线被第三条直线所截，内错角相等． 简单说成：两直线平行，内错角相等．
练习册系列答案
相关题目
星期天的早晨，小明步行从家出发，到离家1050m的书店买书．出发1分钟后，他到达离家150m的地方，又过一分钟后，小明加快了速度．如图，是小明从家出发后，小明离家的路程y（米）与他行驶时间x（分钟）之间的函数图象．根据图象回答问题：
19．
如图是一个“数值转换机”的示意图，若输入x，y的值分别为4，-2，则输出的结果是（ ）
如图是一个“数值转换机”的示意图，若输入x，y的值分别为4，-2，则输出的结果是（ ）| A． | 15 | B． | 5 | C． | -5 | D． | -15 |
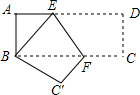如图，长方形ABCD中，AD=8cm，AB=4cm，沿EF折叠，使点D落到点B处，点C落到点C′处
18．
如图，在等腰△ABC中，AB=AC，∠A=20°，AB上一点D使AD=BC，过点D作DE∥BC且DE=AB，连接EC，则∠DCE的度数为（ ）
如图，在等腰△ABC中，AB=AC，∠A=20°，AB上一点D使AD=BC，过点D作DE∥BC且DE=AB，连接EC，则∠DCE的度数为（ ）| A． | 80° | B． | 70° | C． | 60° | D． | 45° |