题目内容
15．先化简：（$\frac{{m}^{2}}{m-2}$-$\frac{4}{m-2}$）÷$\frac{{m}^{2}+2m}{m-1}$，再选择一个你喜欢又使原式有意义的数代入求值．分析 先化简，再把使分母不为0的数代入计算即可．
解答 解：原式=$\frac{（m+2）（m-2）}{m-2}$•$\frac{m-1}{m（m+2）}$
=$\frac{m-1}{m}$，
∵m-2≠0，m-1≠0，m（m+2）≠0，
∴m≠2，1，0，-2，
∴把m=-1代入原式=$\frac{-1-1}{-1}$=2．
点评 本题考查了分式的化简求值，掌握因式分解是解题的关键．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
如图，在四边形ABCD中，∠A=∠D=90°，AD=14，AB=4，CD=6，P是AD上的动点，连接BP，CP，若△PAB∽△CDP，则这样的点P共有（ ）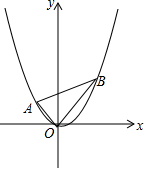
如图，二次函数y=$\frac{2}{3}$x2-$\frac{1}{3}$x，图象过△ABC三个顶点，其中A（-1，m），B（n，n）
如图，在圆内接四边形ABCD中，∠A=52.5°，∠B=97.5°，∠AOB=120°（O为圆心），AB=a，BC=b，CD=c，DA=d，用a、b、c、d表示四边形ABCD的面积．
