题目内容
已知∠MAN=120°,AC平分∠MAN.
(1)如图1,若∠ABC=∠ADC=90°,求证:AD+AB=AC;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论AB+AD=AC是否仍然成立?若成立,给出证明;若不成立,请说明理由.
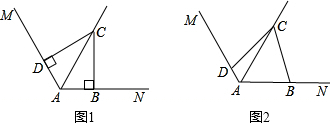
(1)如图1,若∠ABC=∠ADC=90°,求证:AD+AB=AC;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论AB+AD=AC是否仍然成立?若成立,给出证明;若不成立,请说明理由.

考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:(1)根据AC平分∠MAN,可得CB=CD,∠CAB=60°,即可证明RT△ACD≌RT△ACB,可得AD=AB,再根据AC=2AB,即可解题;
(2)根据AC平分∠MAN,可得CB=CD,∠CAB=60°,易证∠FCD=∠BCE,即可证明△CDF≌△CBE,可得BE=DF,再根据(1)中证明AC=AE+AF,即可解题.
(2)根据AC平分∠MAN,可得CB=CD,∠CAB=60°,易证∠FCD=∠BCE,即可证明△CDF≌△CBE,可得BE=DF,再根据(1)中证明AC=AE+AF,即可解题.
解答:证明:(1)∵AC平分∠MAN,
∴CB=CD,∠CAB=60°,
在RT△ACD和RT△ACB中,
,
∴RT△ACD≌RT△ACB(HL),
∴AD=AB,
∵∠ACB=90°-∠CAB=30°,
∴AC=2AB,
∴AD+AB=AC;
(2)成立,过C作CE⊥AN于E,CF⊥AM于F,

∵AC平分∠MAN,
∴CB=CD,∠CAB=60°,
∵∠ABC+∠ADC=180°,
∴∠DCB=60°,
∵∠FCE=180°-∠BAD=60°,
∴∠FCE=∠BCD,
∵∠FCD+∠DCE=∠FCE,∠BCE+∠DCE=∠BCD,
∴∠FCD=∠BCE,
在△CDF和△CBE中,
,
∴△CDF≌△CBE,(ASA)
∴BE=DF,
∴AD+AB=AD+AE+BE=AD+DF+AE=AE+AF,
∵AC=AE+AF,
∴AD+AB=AC.
∴CB=CD,∠CAB=60°,
在RT△ACD和RT△ACB中,
|
∴RT△ACD≌RT△ACB(HL),
∴AD=AB,
∵∠ACB=90°-∠CAB=30°,
∴AC=2AB,
∴AD+AB=AC;
(2)成立,过C作CE⊥AN于E,CF⊥AM于F,

∵AC平分∠MAN,
∴CB=CD,∠CAB=60°,
∵∠ABC+∠ADC=180°,
∴∠DCB=60°,
∵∠FCE=180°-∠BAD=60°,
∴∠FCE=∠BCD,
∵∠FCD+∠DCE=∠FCE,∠BCE+∠DCE=∠BCD,
∴∠FCD=∠BCE,
在△CDF和△CBE中,
|
∴△CDF≌△CBE,(ASA)
∴BE=DF,
∴AD+AB=AD+AE+BE=AD+DF+AE=AE+AF,
∵AC=AE+AF,
∴AD+AB=AC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CDF≌△CBE是解题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
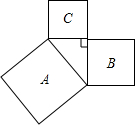 如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )
如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )| A、12 | B、13 | C、144 | D、19 |
 如图,∠AOD=115°,OB是∠AOC的平分线,∠COD=27°,则∠BOD的度数为( )
如图,∠AOD=115°,OB是∠AOC的平分线,∠COD=27°,则∠BOD的度数为( )| A、88° | B、71° |
| C、44° | D、72° |
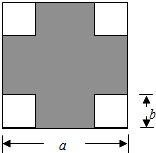 如图,在一块边长为a的正方形纸板四角,各剪去一个边长为b(b<
如图,在一块边长为a的正方形纸板四角,各剪去一个边长为b(b<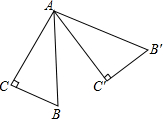 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转70°后得到△AB′C′,则∠CAB′=
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转70°后得到△AB′C′,则∠CAB′= 如图,一条河流两岸是平行的.当小船行驶到河中点E时,与两岸码头B、D成64°角;当小船行驶到河中点F时,看点B和点D的视线FB、FD恰好有∠1=∠2、∠3=∠4的关系.你能说出此时点F与码头B、D形成的∠BFD的度数吗?
如图,一条河流两岸是平行的.当小船行驶到河中点E时,与两岸码头B、D成64°角;当小船行驶到河中点F时,看点B和点D的视线FB、FD恰好有∠1=∠2、∠3=∠4的关系.你能说出此时点F与码头B、D形成的∠BFD的度数吗?