题目内容
3. 一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).(1)如图,3x+3y=12,的图象为直线m,其与x轴交点A的坐标为(4,0),其与y轴交点B的坐标为(0,4);
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-$\frac{5}{3}$,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
分析 (1)分别令3x+3y=12中y=0、x=0求出与之相对应的x、y值,由此即可得出点A、B的坐标;
(2)将x=1代入3x+3y=12中求出y值,即可得出点P的坐标,由点C、P的坐标利用待定系数法即可求出a、b的值.
解答 解:(1)令3x+3y=12中y=0,则3x=12,解得:x=4,
∴A(4,0);
令3x+3y=12中x=0,则3y=12,解得:y=4,
∴B(0,4).
故答案为:(4,0);(0,4).
(2)令3x+3y=12中x=1,则3+3y=12,解得:y=3,
∴P(1,3).
将C(-$\frac{5}{3}$,0)、P(1,3)代入ax+by=-5中,
得:$\left\{\begin{array}{l}{-\frac{5}{3}a=-5}\\{a+3b=-5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=3}\\{b=-\frac{8}{3}}\end{array}\right.$.
点评 本题考查了一次函数图象上点的坐标特征以及待定系数法求函数解析式,解题的关键是:(1)分别令3x+3y=12中y=0、x=0;(2)利用待定系数法求出a、b值.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标,利用待定系数法求出函数解析式是关键.

练习册系列答案
相关题目
15. 如图,在?ABCD中,CE⊥AB,且E为垂足.如果∠D=75°,则∠BCE=( )
如图,在?ABCD中,CE⊥AB,且E为垂足.如果∠D=75°,则∠BCE=( )
 如图,在?ABCD中,CE⊥AB,且E为垂足.如果∠D=75°,则∠BCE=( )
如图,在?ABCD中,CE⊥AB,且E为垂足.如果∠D=75°,则∠BCE=( )| A. | 105° | B. | 15° | C. | 30° | D. | 25° |
18.学校举行运动会,小明用1000元购买书包和文具盒共30个,已知书包每个40元,文具盒每个10元,那么小明最少买文具盒( )
| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
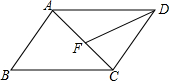 如图,四边形ABCD是平行四边形,∠BAC=80°,DF是∠CDA的角平分线,交AC于点F,∠CDF=25°,则∠CAD=50°.
如图,四边形ABCD是平行四边形,∠BAC=80°,DF是∠CDA的角平分线,交AC于点F,∠CDF=25°,则∠CAD=50°.