题目内容
10.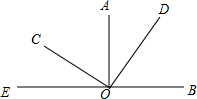 如图,已知AO⊥BE于O点,CO⊥DO于O点,∠BOC=α,则∠AOD的度数为( )
如图,已知AO⊥BE于O点,CO⊥DO于O点,∠BOC=α,则∠AOD的度数为( )| A. | α-90° | B. | 2α-90° | C. | 180°-α | D. | 2α-180° |
分析 首先根据垂直定义可得∠COD=90°,∠AOB=90°,再根据同角的余角相等可得∠BOD=∠AOC,再有条件∠BOC=α,可表示出∠BOD=∠AOC的度数,进而得到答案.
解答 解:∵AO⊥BE,CO⊥DO,
∴∠COD=90°,∠AOB=90°,
即:∠AOD+∠BOD=∠AOD+∠AOC=90°,
∴∠BOD=∠AOC,
∵∠BOC=α,
∴∠BOD=∠AOC=α-90°,
∴∠AOD=90°-α+90°=180°-α,
故选:C.
点评 此题主要考查了余角和补角,关键是掌握余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
20.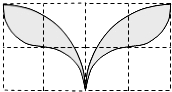 如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )
 如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )| A. | 4π-2 | B. | 2π-2 | C. | 4π-4 | D. | 2π-4 |
5.如果8排6座记作(8,6),那么(3,5)表示( )
| A. | 3排5座 | B. | 5排3座 | C. | 5排5座 | D. | 3排3座 |
2.已知圆锥的底面半径为4cm,高为3cm,则圆锥的侧面积是( )
| A. | 20cm2 | B. | 20πcm2 | C. | 12πcm2 | D. | 10πcm2 |
19.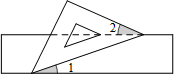 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )| A. | 30° | B. | 45° | C. | 25° | D. | 15° |
 如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.
如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.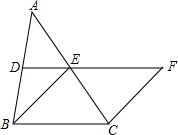 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF