题目内容
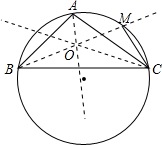 已知点O为△ABC内心,BO的延长线与AC交于N,与△ABC外接圆交于点M,若MC=10,求OM长.
已知点O为△ABC内心,BO的延长线与AC交于N,与△ABC外接圆交于点M,若MC=10,求OM长.考点:三角形的内切圆与内心
专题:
分析:根据三角形的内心是角平分线的交点,以及三角形的外角的性质,即可证得∠MOC=∠MCO,根据等角对等边,即可求解.
解答:解:∵O为△ABC内心,
∴∠ABM=∠MBC,∠ACO=∠BOC,
又∵∠ABM=∠ACM,∠MOC=∠MBC+∠BOC,
∴∠MOC=∠MCO,
∴MO=MC=10.
∴∠ABM=∠MBC,∠ACO=∠BOC,
又∵∠ABM=∠ACM,∠MOC=∠MBC+∠BOC,
∴∠MOC=∠MCO,
∴MO=MC=10.
点评:本题考查了三角形的内心的性质,以及三角形的外角的性质,正确证明∠MOC=∠MCO是关键.

练习册系列答案
相关题目
 小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
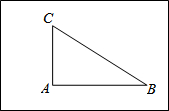
小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上. 已知,如图,AB⊥BD于B,ED⊥BD于D,且AB=CD,AC=CE.求证:(1)△ABC≌△CDE;(2)AC⊥CE.
已知,如图,AB⊥BD于B,ED⊥BD于D,且AB=CD,AC=CE.求证:(1)△ABC≌△CDE;(2)AC⊥CE. 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( )
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( ) 如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.
如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.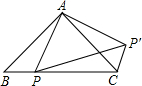 如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′=
如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′=