题目内容

△ABC中，AD为中线，且△ABD的面积为3，则△ACD的面积为
 
．
考点：三角形的面积
专题：
分析：根据等底等高的三角形的面积相等可知三角形的中线把三角形分成面积相等的两个三角形解答．
解答：解：∵AD为中线，
∴S△ABD=S△ACD，
∵△ABD的面积为3，
∴△ACD的面积为3．
故答案为：3．
点评：本题考查了三角形的面积，熟记三角形的中线把三角形分成面积相等的两个三角形是解题的关键．
练习册系列答案
相关题目
计算：32-1=
 
；52-32=
 
；72-52=
 
；92-72=
 
；…
（1）根据以上的计算，你发现什么规律，请用含n的式子表示；
（2）用分解因式的知识说明你发现的规律．
若-1＜a＜0，0＜b＜2，求|a|+|b|-|a+b|-|a-b|．
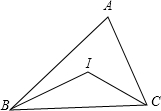如图，在△ABC中，∠A=72°，点I是△ABC内的一点．
（1）若点I是△ABC的内心，求∠BIC的度数；
（2）若点I是△ABC的外心，求∠BIC的度数．
如图，在△ABC中，BC=a，AC=b，AB=c，∠C=90°，CD和BE是△ABC的两条中线，且CD⊥BE，则a：b：c=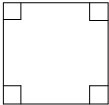
 
．
如图：面积为48cm2的正方形四个角是面积为3cm2的小正方形，现将四个角剪掉，制作一个无盖的长方体盒子，求这个长方体盒子的底面边长和体积分别是多少？（精确到0.1cm，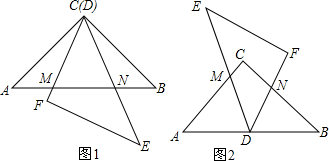
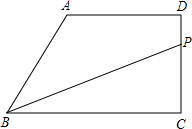3
≈1.732）
小明将两个全等的等腰三角板摆放在一起，其中∠ACB=∠DFE=90°，AB=DE=12．
（1）如图1，当D与C点重合时，CF、CE分别与AB交于M、N两点，且量得AM=3，BN=4，小明发现AM、MN、BN存在某种数量关系，他想：当AM=a，BN=b，MN=c时，这种数量关系仍成立吗？请你一起探究并证明这个结论；
（2）如图2，当等腰Rt△DEF的顶点D恰好在AB的中点处时，DE、DF分别与AC、BC交于M、N，小明经测量后猜想，AM•BN是一个定值．你认可他的猜想吗？说明理由，若猜想成立，请求出该定值．
（3）在（2）的条件下，△DEF绕点D旋转，DE、DF所在的直线分别交线段AC和线段BC于点M、N，若CN=2
2
，求MN的长．
已知：直角梯形ABCD中，DC⊥BC，AD∥BC，AD=AB=5，BC=8．动点P以1个单位/秒的速度从C开始，沿C-D-A方向运动，到达点A时停止．
（1）设△BCP的面积为y，运动的时间为t秒．求y关于t的函数关系式，并写出t的范围；
（2）连接AP，当点P在CD上时，求在第几秒时，△ABP的面积与△BCP的面积相等？
（3）若在点P从点C出发的同时，另一动点M从A开始沿着A-D-C方向运动，运动速度为2个单位/秒．求当P、M相遇时，△BCP的面积？
已知圆锥的底面半径为6，侧面积为60π，则这个圆锥的母线为（　　）
A、6B、8C、10D、12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网