题目内容
 如图,在△ABC中,BC=a,AC=b,AB=c,∠C=90°,CD和BE是△ABC的两条中线,且CD⊥BE,则a:b:c=
如图,在△ABC中,BC=a,AC=b,AB=c,∠C=90°,CD和BE是△ABC的两条中线,且CD⊥BE,则a:b:c=考点:勾股定理,三角形的重心
专题:
分析:设BE和CD相交于O,根据三角形的重心得出OC=
CD=
×
c=
c,OB=
BE=
,然后根据勾股定理得出OC2+OB2=BC2,AC2+BC2=AB2,即
c2+b2=5a2,a2+b2=c2,解得c=
a,b=
a,即可求得a:b:c的值.
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
a2+(
|
c2+b2=5a2,a2+b2=c2,解得c=
| 3 |
| 2 |
解答:解:设BE和CD相交于O,则∠BOC=90°,
∵CD和BE是△ABC的两条中线,
∴CD=AD=DB=
AB=
c,BE=
,
∵O是三角形的重心,
∴OC=
CD=
×
c=
c,OB=
BE=
,
∵OC2+OB2=BC2,
∴(
c)2+(
)2=a2,
整理得:c2+b2=5a2,
又a2+b2=c2,
解得:c=
a,b=
a,
∴a:b:c=1:
:
.
故答案为1:
:
.
∵CD和BE是△ABC的两条中线,
∴CD=AD=DB=
| 1 |
| 2 |
| 1 |
| 2 |
a2+(
|
∵O是三角形的重心,
∴OC=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
a2+(
|
∵OC2+OB2=BC2,
∴(
| 1 |
| 3 |
| 2 |
| 3 |
a2+(
|
整理得:c2+b2=5a2,
又a2+b2=c2,
解得:c=
| 3 |
| 2 |
∴a:b:c=1:
| 2 |
| 3 |
故答案为1:
| 2 |
| 3 |
点评:本题考查了三角形的重心的性质,勾股定理的应用,勾股定理的应用是本题的关键.

练习册系列答案
相关题目
美国NBA职业篮球赛的两支队伍在本赛季已进行了5场比赛,根据统计,两队5场比赛得分的频数分布直方图如下所示,则得分方差较小的队伍是( )


| A、甲 | B、乙 | C、一样大 | D、无法确定 |
 已知点A、B、C在⊙O上,连接AB、AC、BC,若∠A=90°,求证:BC为⊙O的直径.
已知点A、B、C在⊙O上,连接AB、AC、BC,若∠A=90°,求证:BC为⊙O的直径. 如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC的度数为
如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC的度数为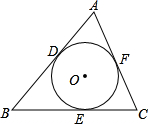 已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.
已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长. 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有 如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.