题目内容
若-1<a<0,0<b<2,求|a|+|b|-|a+b|-|a-b|.
考点:整式的加减,绝对值
专题:
分析:首先根据a、b的取值范围确定a+b>0,a-b<0,再根据绝对值的性质去掉绝对值符号,合并同类项即可.
解答:解:∵-1<a<0,0<b<2,
∴a+b>0,a-b<0,
∴|a|+|b|-|a+b|-|a-b|=-a+b-a-b+a-b=-a-b.
∴a+b>0,a-b<0,
∴|a|+|b|-|a+b|-|a-b|=-a+b-a-b+a-b=-a-b.
点评:此题主要考查了整式的加减,以及绝对值的性质,关键是掌握:
①当a是正有理数时,a的绝对值是它本身a;
②当a是负有理数时,a的绝对值是它的相反数-a;
③当a是零时,a的绝对值是零.
①当a是正有理数时,a的绝对值是它本身a;
②当a是负有理数时,a的绝对值是它的相反数-a;
③当a是零时,a的绝对值是零.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC的度数为
如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC的度数为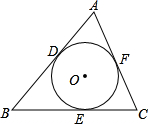 已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.
已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.