题目内容
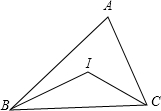 如图,在△ABC中,∠A=72°,点I是△ABC内的一点.
如图,在△ABC中,∠A=72°,点I是△ABC内的一点.(1)若点I是△ABC的内心,求∠BIC的度数;
(2)若点I是△ABC的外心,求∠BIC的度数.
考点:三角形的内切圆与内心,三角形的外接圆与外心
专题:
分析:(1)根据三角形内角和定理求得∠ABC+∠ACB的值,然后根据角平分线的定义求得∠IBC+∠ICB,最后利用三角形内角和定理求解;
(2)根据圆周角定理即可求解.
(2)根据圆周角定理即可求解.
解答:解:(1)∵△ABC中,∠ABC+∠ACB=180°-∠A=180°-72°=108°,
又∵I是△ABC的内心,即∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠IBC+∠ICB=
×108°=54°,
∴∠BIC=180°-(∠IBC+∠ICB)=180°-54°=126°;
(2)∵点I是△ABC的外心,
∴∠BIC=2∠A=2×72°=144°.
又∵I是△ABC的内心,即∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠IBC+∠ICB=
| 1 |
| 2 |
∴∠BIC=180°-(∠IBC+∠ICB)=180°-54°=126°;
(2)∵点I是△ABC的外心,
∴∠BIC=2∠A=2×72°=144°.
点评:本题考查了三角形的内心和外心,以及圆周角定理,正确理解内心的定义是关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
已知⊙O中,
=3
,则弦AB和3CD的大小关系是( )
 |
| AB |
 |
| CD |
| A、AB>3CD |
| B、AB=3CD |
| C、AB<3CD |
| D、不能确定 |
 已知AB∥CD,BC平分∠ACD.求证:AC=AB.
已知AB∥CD,BC平分∠ACD.求证:AC=AB.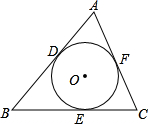 已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.
已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.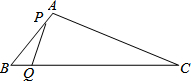 如图,在△ABC中,AB=10cm.BC=20cm、点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过几秒钟后,以P、B、Q三点为顶点的三角形与△ABC相似?
如图,在△ABC中,AB=10cm.BC=20cm、点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过几秒钟后,以P、B、Q三点为顶点的三角形与△ABC相似?