题目内容
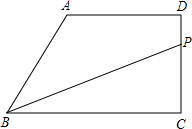 已知:直角梯形ABCD中,DC⊥BC,AD∥BC,AD=AB=5,BC=8.动点P以1个单位/秒的速度从C开始,沿C-D-A方向运动,到达点A时停止.
已知:直角梯形ABCD中,DC⊥BC,AD∥BC,AD=AB=5,BC=8.动点P以1个单位/秒的速度从C开始,沿C-D-A方向运动,到达点A时停止.(1)设△BCP的面积为y,运动的时间为t秒.求y关于t的函数关系式,并写出t的范围;
(2)连接AP,当点P在CD上时,求在第几秒时,△ABP的面积与△BCP的面积相等?
(3)若在点P从点C出发的同时,另一动点M从A开始沿着A-D-C方向运动,运动速度为2个单位/秒.求当P、M相遇时,△BCP的面积?
考点:四边形综合题
专题:
分析:(1)过点A作AE⊥BC于点E,根据勾股定理可得出AE的长,进而得出CD的长,根据三角形的面积公式即可得出结论;
(2)先求出梯形ABCD的面积,设在第x秒时,△ABP的面积与△BCP的面积相等,即S△BCP=S梯形ABC-S△BCP-S△ADP,由此可得出结论;
(3)设经过t秒P、M相遇,求出t的值,进而得出结论.
(2)先求出梯形ABCD的面积,设在第x秒时,△ABP的面积与△BCP的面积相等,即S△BCP=S梯形ABC-S△BCP-S△ADP,由此可得出结论;
(3)设经过t秒P、M相遇,求出t的值,进而得出结论.
解答: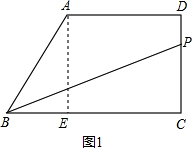 解:(1)如图1,过点A作AE⊥BC于点E,
解:(1)如图1,过点A作AE⊥BC于点E,
∵DC⊥BC,AD∥BC,AD=AB=5,BC=8,
∴BE=3,
∴AE=
=
=4,
∴CD=AE=4,
∴当点P在CD上时,y=
BC•t=4t(0<t≤4);
当点P在AD上时,y=
BC•CD=
×8×4=16(4<t≤9).
故
;
(2)如图2,∵直角梯形ABCD中,DC⊥BC,AD∥BC,AD=AB=5,BC=8,CD=4,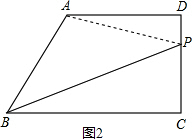
∴S梯形ABC=
(AD+BC)•CD=
(5+8)×4=26,
设在第x秒时,△ABP的面积与△BCP的面积相等,即S△BCP=S梯形ABC-S△BCP-S△ADP,
∴
BC•x=26-
BC•x-
AD•(4-x),即
×8x=26-
×8x-
×5×(4-x),解得x=
(秒).
答:在第
秒时,△ABP的面积与△BCP的面积相等;
(3)设经过t秒P、M相遇,
∵点P从点C出发的同时,另一动点M从A开始沿着A-D-C方向运动,运动速度为2个单位/秒,AD=5,CD=4,
∴3t=AD+CD=5+4=9,解得t=3(秒),
∴S△BCP=
BC×3=
×8×3=12.
答:△BCP的面积为12.
 解:(1)如图1,过点A作AE⊥BC于点E,
解:(1)如图1,过点A作AE⊥BC于点E,∵DC⊥BC,AD∥BC,AD=AB=5,BC=8,
∴BE=3,
∴AE=
| AB2-BE2 |
| 52-32 |
∴CD=AE=4,
∴当点P在CD上时,y=
| 1 |
| 2 |
当点P在AD上时,y=
| 1 |
| 2 |
| 1 |
| 2 |
故
|
(2)如图2,∵直角梯形ABCD中,DC⊥BC,AD∥BC,AD=AB=5,BC=8,CD=4,

∴S梯形ABC=
| 1 |
| 2 |
| 1 |
| 2 |
设在第x秒时,△ABP的面积与△BCP的面积相等,即S△BCP=S梯形ABC-S△BCP-S△ADP,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 32 |
| 11 |
答:在第
| 32 |
| 11 |
(3)设经过t秒P、M相遇,
∵点P从点C出发的同时,另一动点M从A开始沿着A-D-C方向运动,运动速度为2个单位/秒,AD=5,CD=4,
∴3t=AD+CD=5+4=9,解得t=3(秒),
∴S△BCP=
| 1 |
| 2 |
| 1 |
| 2 |
答:△BCP的面积为12.
点评:本题考查的是四边形综合题,涉及到梯形及直角三角形的面积公式,难度适中.

练习册系列答案
相关题目
 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有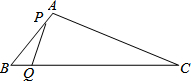 如图,在△ABC中,AB=10cm.BC=20cm、点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过几秒钟后,以P、B、Q三点为顶点的三角形与△ABC相似?
如图,在△ABC中,AB=10cm.BC=20cm、点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过几秒钟后,以P、B、Q三点为顶点的三角形与△ABC相似? 如图,在Rt△ABD中,∠D=90°,BP是∠ABD的平分线.
如图,在Rt△ABD中,∠D=90°,BP是∠ABD的平分线.