题目内容
4.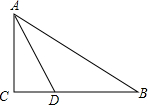 已知,在△ABC中,AD是角平分线,AD=BD,AB=2AC,求证:△ACB是直角三角形.
已知,在△ABC中,AD是角平分线,AD=BD,AB=2AC,求证:△ACB是直角三角形.
分析 过D作DE⊥AC,得到∠AED=90°,由AD是角平分线,得到∠CAD=∠BAD,根据等腰三角形的性质得到AB=2AE,等量代换得到AC=AE,推出△ACD≌△AED,根据全等三角形的性质即可得到结论.
解答 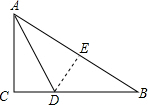 证明:过D作DE⊥AC,
证明:过D作DE⊥AC,
∴∠AED=90°,
∵AD是角平分线,
∴∠CAD=∠BAD,
∵AD=BD,
∴AB=2AE,
∵AB=2AC,
∴AC=AE,
在△ACD与△AED中,
$\left\{\begin{array}{l}{AC=AE}\\{∠CAD=∠EAD}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED,
∴∠ACD=∠AED=90°,
∴△ACB是直角三角形.
点评 本题考查了全等三角形的判定和性质,角平分线的定义,等腰三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
13. 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )| A. | 0,1,-2 | B. | 1,0,-2 | C. | -2,0,1 | D. | 0,-2,1 |
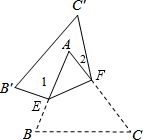 如图,把△ABC沿EF对折,折叠后的图形如图所示.若∠A=60°,∠1=96°,则∠2的度数为24°.
如图,把△ABC沿EF对折,折叠后的图形如图所示.若∠A=60°,∠1=96°,则∠2的度数为24°. 已知如图,AC、BD相交于点O,且被点O互相平分,求证:
已知如图,AC、BD相交于点O,且被点O互相平分,求证: 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.
如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.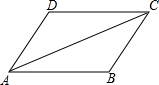 用2根同样长的木条AB,CD和另外两根同样长的木条AD,BC拼成一个四边形ABCD,
用2根同样长的木条AB,CD和另外两根同样长的木条AD,BC拼成一个四边形ABCD, 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).