Question

1．如图，已知：等边三角形ABC中内有一点P，PA=4，PC=3，PB=5，求∠APC的度数．

Answer 1

分析 根据题意，通过顺时针旋转，可以得到△ADB与△APC的关系，通过转化可以求得∠ADB的度数，从而可以求得∠APC的度数．

解答 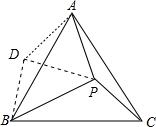解：如图，∵△ABC为等边三角形，
∴AB=AC，∠BAC=60°；
将△APC按顺时针旋转60°，得到△ADB，
∴AD=AP=PD，DB=CP，∠ADB=∠APC，
∴△ADP是等边三角形，
∴∠ADP=60°，
∵AP=4，PC=3，
∴BD=CP=3，PD=AP=4，BP=5，
∵3²+4²=5²，
∴△BDP是直角三角形，∠BDP=90°，
∴∠ADB=∠ADP+∠BDP=60°+90°=150°，
∴∠APC=150°．

点评 本题考查勾股定理的逆定理、等边三角形的性质、旋转的性质，解题的关键是明确题意，利用数形结合的思想解答．