题目内容
3.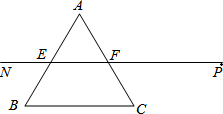 射线PN与等边△ABC的两边AB,BC分别交于点E,F,且BC∥EF,AE=BE=2cm,PF=4cm.动点Q从点P出发,沿射线PN以每秒2cm的速度向左移动,同时△ABC也沿射线PN以每秒1cm的速度向左移动,经过t秒,以点Q为圆心,$\sqrt{3}$cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=2或3≤t≤7或t=8.(单位:秒)
射线PN与等边△ABC的两边AB,BC分别交于点E,F,且BC∥EF,AE=BE=2cm,PF=4cm.动点Q从点P出发,沿射线PN以每秒2cm的速度向左移动,同时△ABC也沿射线PN以每秒1cm的速度向左移动,经过t秒,以点Q为圆心,$\sqrt{3}$cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=2或3≤t≤7或t=8.(单位:秒)
分析 根据⊙Q以每秒2cm的速度向左移动,△ABC也沿射线PN以每秒1cm的速度向左移动,确定⊙Q的相对速度,根据已知条件结合图形,求出t可取的一切值.
解答 解:⊙Q以每秒2cm的速度向左移动,△ABC也沿射线PN以每秒1cm的速度向左移动,
相当于△ABC静止,Q以每秒1cm的速度向左移动,
①当⊙Q与AC相切时,因为半径为$\sqrt{3}$,所以QF=2,则PQ=2,即t=2,
②作CD⊥PN,BH⊥PN,
∵BE=2,∴BH=$\sqrt{3}$,HE=1,
同理,CD=$\sqrt{3}$,DF=1,
∴当⊙Q在由D到H的过程中与BC相切,此时3≤t≤7,
③当⊙Q与AB相切时,因为半径为$\sqrt{3}$,所以GE=2,即t=8,
故答案为:t=2或3≤t≤7或t=8.
点评 本题考查的是直线与圆的位置关系,能够分析出所有相切的情形是解题的关键,解答过程中注意圆心到直线距离与圆的半径相等时,直线与圆相切.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在平行四边形ABCD中,∠A+∠C=240°,则∠B的度数是( )
| A. | 120° | B. | 80° | C. | 100° | D. | 60° |
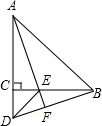 如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.
如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.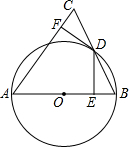 如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.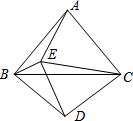 如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°.
如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°. 我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD.
我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD. 把一块矩形直尺与一块直角三角板如图放置,若∠1=40°,则∠2的度数为130°.
把一块矩形直尺与一块直角三角板如图放置,若∠1=40°,则∠2的度数为130°.