题目内容
5.先化简,再求值:(x-2y)2n÷(2y-x)2n-1+(2x-y)(-2x-y)+(x-y)(-x+y),其中x=$\frac{1}{3}$,y=$\frac{2}{3}$.分析 原式第一项变形后利用同底数幂的除法法则计算,第二项利用平方差公式化简,最后一项利用完全平方公式展开,整理得到最简结果,把x与y的值代入计算即可求出值.
解答 解:原式=-(x-2y)2n÷(x-2y)2n-1+(2x-y)(-2x-y)+(x-y)(-x+y)
=-(x-2y)+y2-4x2-x2+2xy-y2
=2xy-5x2-x+2y,
当x=$\frac{1}{3}$,y=$\frac{2}{3}$时,原式=$\frac{4}{9}$-$\frac{5}{9}$-$\frac{1}{3}$+$\frac{4}{3}$=$\frac{8}{9}$.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.某工地因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
13.下列说法中:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点;⑤画射线OA=3cm;⑥经过三点中的两点作直线总共有3条.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.在平行四边形ABCD中,∠A+∠C=240°,则∠B的度数是( )
| A. | 120° | B. | 80° | C. | 100° | D. | 60° |
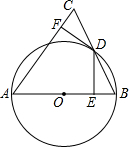 如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.