题目内容
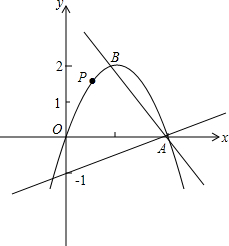 如图,已知过点A的直线AB:y=-2x+4和直线AC:y=
如图,已知过点A的直线AB:y=-2x+4和直线AC:y=| 1 |
| 2 |
(1)直线AC与y轴的交点C的坐标为
(2)求出抛物线的解析式;
(3)点P(m,n)是抛物线上OB间的一点
①作PQ平行于y轴交直线AC于点Q,当线段PQ被x轴平分时,求出点P的坐标;
②作PM⊥AB于M,PN⊥AC于N,四边形PMAN能否为正方形?若能,求出点P的坐标;若不能,请说明理由.
考点:二次函数综合题
专题:
分析:(1)由直线AC:y=
x-1可知当x=0时,y=-1,即可求得直线AC与y轴的交点C的坐标,由于直线AB和直线AC的斜率互为负倒数,所以AB⊥AC,即∠CAB=90°.
(2)利用待定系数法即可求得抛物线的解析式;
(3)过点P作x轴的平行线交AB于E,作y轴的平行线交AC于F,则∠EBF=90°,根据四边形PMAN为正方形,得出PM=PN,根据∠MPN=∠EPF=90°,得出∠MPE=∠NPF,进而求得△MPE≌△NPF,得出PE=PF,设P的坐标为(m,-2m2+4m),则E(m2-2m+2,-2m2+4m),F(m,
m-1),根据PE=PF得出关于m的方程,解方程即可求得m的值,进而求得P的坐标.
| 1 |
| 2 |
(2)利用待定系数法即可求得抛物线的解析式;
(3)过点P作x轴的平行线交AB于E,作y轴的平行线交AC于F,则∠EBF=90°,根据四边形PMAN为正方形,得出PM=PN,根据∠MPN=∠EPF=90°,得出∠MPE=∠NPF,进而求得△MPE≌△NPF,得出PE=PF,设P的坐标为(m,-2m2+4m),则E(m2-2m+2,-2m2+4m),F(m,
| 1 |
| 2 |
解答:解:(1)由直线AC:y=
x-1可知直线AC与y轴的交点C的坐标为 (0,-1),
由直线AB:y=-2x+4的斜率为-2,直线AC:y=
x-1的斜率为
,可知AB⊥AC,
所以∠CAB=90°.
(2)解
得
,
∴A(2,0),
∵抛物线经过A、B、O三点,设抛物线的解析式为y=ax2+bx+c(a≠0),
∴
,
解得
.
∴抛物线的解析式为y=-2x2+4x.
(3)如图,过点P作x轴的平行线交AB于E,作y轴的平行线交AC于F,则∠EBF=90°,
∵PM⊥AB于M,PN⊥AC,AB⊥AC,
∴四边形PMAN是矩形,
设P的坐标为(m,-2m2+4m),则E(m2-2m+2,-2m2+4m),F(m,
m-1),
∵四边形PMAN为正方形,
∴PM=PN,
∵∠MPN=∠EPF=90°,
∴∠MPE=∠NPF,
在△MPE和△NPF中,
,
∴△MPE≌△NPF(AAS),
∴PE=PF,
∴m2-2m+2-m=-2m2+4m-
m+1,
解得,m=
,或m=2(舍去),
∴P(
,
).
| 1 |
| 2 |
由直线AB:y=-2x+4的斜率为-2,直线AC:y=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠CAB=90°.
(2)解
|
|
∴A(2,0),
∵抛物线经过A、B、O三点,设抛物线的解析式为y=ax2+bx+c(a≠0),
∴
|
解得
|
∴抛物线的解析式为y=-2x2+4x.
(3)如图,过点P作x轴的平行线交AB于E,作y轴的平行线交AC于F,则∠EBF=90°,
∵PM⊥AB于M,PN⊥AC,AB⊥AC,
∴四边形PMAN是矩形,

设P的坐标为(m,-2m2+4m),则E(m2-2m+2,-2m2+4m),F(m,
| 1 |
| 2 |
∵四边形PMAN为正方形,
∴PM=PN,
∵∠MPN=∠EPF=90°,
∴∠MPE=∠NPF,
在△MPE和△NPF中,
|
∴△MPE≌△NPF(AAS),
∴PE=PF,
∴m2-2m+2-m=-2m2+4m-
| 1 |
| 2 |
解得,m=
| 1 |
| 6 |
∴P(
| 1 |
| 6 |
| 11 |
| 18 |
点评:本题考查了直线的交点,直线与坐标轴交点的特征,待定系数法求解析式,三角形全等的判定和性质,正方形的性质等,(3)三角形全等是本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
平面内有三个点,过任意两点画一条直线,则可以画直线的条数( )
| A、2条 | B、3条 |
| C、4条 | D、1条或3条 |
 如图,在此图中小于平角的角有( )个.
如图,在此图中小于平角的角有( )个.| A、8 | B、9 | C、10 | D、11 |
当x=-2时,代数式x2-1的值为( )
| A、-5 | B、5 | C、-3 | D、3 |
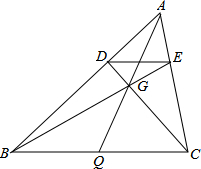 在△ABC中,作DE∥BC,连BE、CD交于一点G,连AG延长至BC上于Q.证明:Q是BC中点.
在△ABC中,作DE∥BC,连BE、CD交于一点G,连AG延长至BC上于Q.证明:Q是BC中点.