题目内容
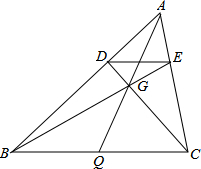在△ABC中，作DE∥BC，连BE、CD交于一点G，连AG延长至BC上于Q．证明：Q是BC中点．考点：平行线分线段成比例
专题：证明题
分析：利用平行线分线段成比例定理的性质以及三角形面积公式求出S△BAG=S△CAG，进而得出S△BGQ=S△CGQ，求出即可．
解答：
证明：∵△BDE与△CED有共同的底DE，且DE∥BC，
∴S△BDE=S△CED，
∴S△BDE-S△GDE=S△CED-S△GDE，
∴S△BDG=S△CEG①，
∵DE∥BC，
∴
=
，
而
=
，
=
，
∴
=
②，
由①与②得：S△ADG=S△AED③，
由①+③得：S△BAG=S△CAG④，
过C、B作直线AQ的垂线，K、H为垂足（如图），
则S△BAG=
×AG×BH，S△BAG=
×AG×CK，代入④得：BH=CK，
故
GQ×BH=
GQ×KC，即S△BGQ=S△CGQ，
而△BGQ与△CGQ有公共顶点G，底BQ与CQ在同一直线上，
故BQ=QC．
证明：∵△BDE与△CED有共同的底DE，且DE∥BC，∴S△BDE=S△CED，
∴S△BDE-S△GDE=S△CED-S△GDE，
∴S△BDG=S△CEG①，
∵DE∥BC，
∴
| AD |
| DB |
| AE |
| EC |
而
| S△ADG |
| S△BDG |
| AD |
| DB |
| S△AEG |
| S△CGE |
| AE |
| EC |
∴
| S△ADG |
| S△BDG |
| S△AEG |
| S△CGE |
由①与②得：S△ADG=S△AED③，
由①+③得：S△BAG=S△CAG④，
过C、B作直线AQ的垂线，K、H为垂足（如图），
则S△BAG=
| 1 |
| 2 |
| 1 |
| 2 |
故
| 1 |
| 2 |
| 1 |
| 2 |
而△BGQ与△CGQ有公共顶点G，底BQ与CQ在同一直线上，
故BQ=QC．
点评：此题主要考查了平行线分线段成比例定理以及三角形面积求法，得出S△BAG=S△CAG是解题关键．
练习册系列答案
相关题目
泉州向北京打长途电话，通话3分钟以内3.6元，每超过1分钟加收1元，某人打电话x分钟（x＞3的整数）则应付电话费（ ）
| A、3.6x元 |
| B、（3.6+x）元 |
| C、（0.6+x）元 |
| D、（x-3.6）元 |
计算（-x）4÷x2•x2的结果是（ ）
| A、1 |
| B、-1 |
| C、x4 |
| D、-x4 |
下列各式中不成立的是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、（
|
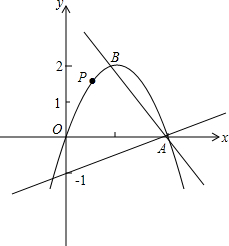如图，已知过点A的直线AB：y=-2x+4和直线AC：y=
如图，PC经过圆心O，弦AB⊥PC于点D．连接BC和PA，且∠PAB=2∠PCB．
如图，在矩形ABCD中，点E是AD上一点，点F是AB上一点，EF=CE且EF⊥CE，求证：AE=AB．