题目内容
x2+
+2(x+
)=1.
| 1 |
| x2 |
| 1 |
| x |
考点:换元法解一元二次方程
专题:计算题
分析:先利用完全平方公式把原方程变形得到(x+
)2+2(x+
)-3=0,则可利用换元法解方程:设x+
=t,原方程化为t2+2t-3=0,解得t1=-3,t2=1,
然后分别解方程x+
=-3和x+
=1即可得到原方程的解.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
然后分别解方程x+
| 1 |
| x |
| 1 |
| x |
解答:解:(x+
)2-2+2(x+
)=1,即(x+
)2+2(x+
)-3=0,
设x+
=t,
原方程化为t2+2t-3=0,解得t1=-3,t2=1,
当t=-3时,x+
=-3,解得x1=
,x2=
;
当t=1时,x+
=1,此方程无实数解,
所以原方程的解为x1=
,x2=
.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
设x+
| 1 |
| x |
原方程化为t2+2t-3=0,解得t1=-3,t2=1,
当t=-3时,x+
| 1 |
| x |
-3+
| ||
| 2 |
-3-
| ||
| 2 |
当t=1时,x+
| 1 |
| x |
所以原方程的解为x1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
点评:本题考查了换元法解一元二次方程:把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.

练习册系列答案
相关题目
 若a,b在数轴上表示如图所示,那么( )
若a,b在数轴上表示如图所示,那么( )| A、a<b |
| B、a-b<0 |
| C、|a-b|=-(a-b) |
| D、|b-a|=a-b |
甲厂的年产值为7450万元,比乙厂的年产值的5倍还多420万元,若设乙厂的年产值为x万元,下列所列方程中错误的是( )
| A、5x+420=7450 |
| B、7450-5x=420 |
| C、7450-(5x+420)=0 |
| D、5x-420=7450 |
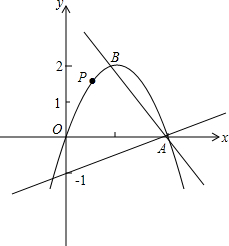 如图,已知过点A的直线AB:y=-2x+4和直线AC:y=
如图,已知过点A的直线AB:y=-2x+4和直线AC:y= 如图,PC经过圆心O,弦AB⊥PC于点D.连接BC和PA,且∠PAB=2∠PCB.
如图,PC经过圆心O,弦AB⊥PC于点D.连接BC和PA,且∠PAB=2∠PCB.