题目内容
4.用直接开平方法解方程(x+m)2=n,下列结论正确的是( )| A. | 有两个根,为x=±$\sqrt{n}$ | B. | 当n≥0时,有两个解,为x=±$\sqrt{n}$-m | ||
| C. | 当n≥0时,有两个解,为x=±$\sqrt{n-m}$ | D. | 当n≤0时,无实数解 |
分析 根据一个数的平方是非负数,可得n≥0,用直接开平方法求得x=±$\sqrt{n}$-m,然后对照四个选项即可解答.
解答 解:∵(x+m)2≥0,
∴n≥0.
∴当n≥0时,方程(x+m)2=n有两个根x=±$\sqrt{n}$-m,
故选B.
点评 本题考查了用直接开方法求一元二次方程的解,基本形式有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
12. 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | $\left\{{\begin{array}{l}{x>1}\\{x>-2}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x≥1}\\{x>-2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x≤1}\\{x<-2}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x<1}\\{x<-2}\end{array}}\right.$ |
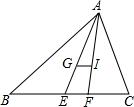 在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.
在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.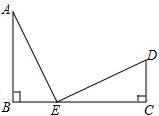 如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.
如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论. 如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π)
如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π)