题目内容
15.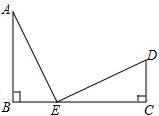 如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.
如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.
分析 先根据AB⊥BC得出∠B=90°,再由△ABE≌△ECD可知∠A=∠DEC,∠AEB=∠EDC,∠B=∠C=90°,由∠A+∠AEB=90°,∠DEC+∠D=90°可知∠AEB+∠DEC=90°,故∠AED=90°,由此可得出结论.
解答 解:AE⊥DE.
∵AB⊥BC,
∴∠B=90°.
∵△ABE≌△ECD,
∴∠A=∠DEC,∠AEB=∠EDC,∠B=∠C=90°.
∵∠A+∠AEB=90°,∠DEC+∠D=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°,即AE⊥DE.
点评 本题考查的是全等三角形的性质,熟知全等三角形的对应角相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.用直接开平方法解方程(x+m)2=n,下列结论正确的是( )
| A. | 有两个根,为x=±$\sqrt{n}$ | B. | 当n≥0时,有两个解,为x=±$\sqrt{n}$-m | ||
| C. | 当n≥0时,有两个解,为x=±$\sqrt{n-m}$ | D. | 当n≤0时,无实数解 |
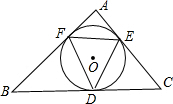 如图:
如图: 已知:如图,AB,AC,AD是⊙O的弦.且∠BAC=∠DAC,弦CE∥AB.求证:CE=AD.
已知:如图,AB,AC,AD是⊙O的弦.且∠BAC=∠DAC,弦CE∥AB.求证:CE=AD.