题目内容
19. 如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π)
如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π)
分析 根据四边形ABCD是正方形,于是得到AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°,设AH=AE=x,则BE=DH=2-x,同时得到CF=CG=x,根据弧长的公式即可得到结果.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°,
设AH=AE=x,则BE=DH=2-x,
∴CF=CG=x,
∴阴影部分的外围的周长=2($\frac{90•π•x}{180}$$+\frac{90•π•(2-x)}{180}$)=2π,
故答案为:2π.
点评 本题考查了相切两圆的性质,正方形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.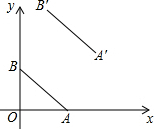 如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )
如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )
 如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )
如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到A′B′,若点A′的坐标为(6,3),则点B′的坐标为( )| A. | (2,6) | B. | (2,5) | C. | (6,2) | D. | (3,6) |
4.用直接开平方法解方程(x+m)2=n,下列结论正确的是( )
| A. | 有两个根,为x=±$\sqrt{n}$ | B. | 当n≥0时,有两个解,为x=±$\sqrt{n}$-m | ||
| C. | 当n≥0时,有两个解,为x=±$\sqrt{n-m}$ | D. | 当n≤0时,无实数解 |
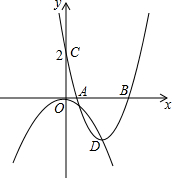 如图,已知抛物线C1:y=-$\frac{1}{2}$x2,平移抛物线y=x2,使其顶点D落在抛物线C1位于y轴右侧的图象上,设平移后的抛物线为C2,且C2与y轴交于点C(0,2).
如图,已知抛物线C1:y=-$\frac{1}{2}$x2,平移抛物线y=x2,使其顶点D落在抛物线C1位于y轴右侧的图象上,设平移后的抛物线为C2,且C2与y轴交于点C(0,2). 已知:如图,AB,AC,AD是⊙O的弦.且∠BAC=∠DAC,弦CE∥AB.求证:CE=AD.
已知:如图,AB,AC,AD是⊙O的弦.且∠BAC=∠DAC,弦CE∥AB.求证:CE=AD.