题目内容
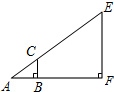 如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=
如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=| 3 |
| 4 |
| A、6.3 | B、7.5 |
| C、8 | D、6.5 |
考点:解直角三角形的应用
专题:
分析:通过解直角△ACB求得AB的长度;结合已知条件得到AF的长度;最后通过解直角△AEF来求线段EF的长度即可.
解答: 解:如图,∵在△ACB中,∠ABC=90°,BC=1.2米,tanA=
解:如图,∵在△ACB中,∠ABC=90°,BC=1.2米,tanA=
,
∴AB=
=
=1.6(米).
又∵BF=8.4米,
∴AF=AB+BF=10米.
又∵在直角△AFE中,∠F=90°,tanA=
,
∴EF=AF•tanA=10×
=7.5(米)
故选:B.
 解:如图,∵在△ACB中,∠ABC=90°,BC=1.2米,tanA=
解:如图,∵在△ACB中,∠ABC=90°,BC=1.2米,tanA=| 3 |
| 4 |
∴AB=
| CB |
| tanA |
| 1.2 | ||
|
又∵BF=8.4米,
∴AF=AB+BF=10米.
又∵在直角△AFE中,∠F=90°,tanA=
| 3 |
| 4 |
∴EF=AF•tanA=10×
| 3 |
| 4 |
故选:B.
点评:本题考查了解直角三角形的应用.解直角三角形的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )| A、两点之间线段最短 |
| B、两点确定一条直线 |
| C、垂线段最短 |
| D、以上都不是 |
 如图所示,阳光照射在一根因暴雨发生地陷而倾斜的电线杆AB上,已知AB的长为6m,此时顶点B到地面的距离BO为3m,某时刻身高为1.8m的小明在阳光下的影长为2.4m,求此时电线杆的影长为多少?
如图所示,阳光照射在一根因暴雨发生地陷而倾斜的电线杆AB上,已知AB的长为6m,此时顶点B到地面的距离BO为3m,某时刻身高为1.8m的小明在阳光下的影长为2.4m,求此时电线杆的影长为多少? 已知A、B两地相距300千米,现有甲、乙两车同时从A地开往B地,先匀速行驶2h到达AB中点C地,停留2h后,再匀速行1.5h到达B地;乙车始终以akm/h(a≠75)的速度行驶.
已知A、B两地相距300千米,现有甲、乙两车同时从A地开往B地,先匀速行驶2h到达AB中点C地,停留2h后,再匀速行1.5h到达B地;乙车始终以akm/h(a≠75)的速度行驶.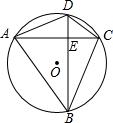 如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少?
如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少? △ABC在平面直角坐标系中的位置如图.
△ABC在平面直角坐标系中的位置如图.