题目内容
 已知A、B两地相距300千米,现有甲、乙两车同时从A地开往B地,先匀速行驶2h到达AB中点C地,停留2h后,再匀速行1.5h到达B地;乙车始终以akm/h(a≠75)的速度行驶.
已知A、B两地相距300千米,现有甲、乙两车同时从A地开往B地,先匀速行驶2h到达AB中点C地,停留2h后,再匀速行1.5h到达B地;乙车始终以akm/h(a≠75)的速度行驶.(1)试设s(km)、t(时)分别表示甲车离开A地的路程和时间,当①0≤t≤2; ②2<t≤4; ③4<t≤5.5时,分别求出s与t的关系式,并在所给的坐标系中画出它的图象;
(2)若甲、乙两车在途中恰好相遇2次(不含A,B两地),试确定a的取值范围.
考点:一次函数的应用
专题:
分析:(1)①根据甲的速度写出函数关系式即可;②根据路程不发生变化解答;③写出t=4和5.5时的坐标,然后利用待定系数法求一次函数解析式解答,再根据一次函数图象的作法画出即可;
(2)判断出在甲停留时第一次相遇,停留后再行驶时第二次相遇列出不等式组,然后求解即可.
(2)判断出在甲停留时第一次相遇,停留后再行驶时第二次相遇列出不等式组,然后求解即可.
解答: 解:(1)①0≤t≤2时,s=
解:(1)①0≤t≤2时,s=
t=150t;
②2<t≤4时,s=150;
③4<t≤5.5时,设s=kt+b,
∵函数图象经过点(4,150),(5.5,300),
∴
,
解得
,
所以,s=100t-250,
函数图象如图所示;
(2)∵甲、乙两车在途中恰好相遇2次,
∴
,
解得
<a<
.
 解:(1)①0≤t≤2时,s=
解:(1)①0≤t≤2时,s=| 300 |
| 2 |
②2<t≤4时,s=150;
③4<t≤5.5时,设s=kt+b,
∵函数图象经过点(4,150),(5.5,300),
∴
|
解得
|
所以,s=100t-250,
函数图象如图所示;
(2)∵甲、乙两车在途中恰好相遇2次,
∴
|
解得
| 75 |
| 2 |
| 600 |
| 11 |
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,难点在于(2)读懂题目信息并列出不等式组.

练习册系列答案
相关题目
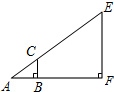 如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=
如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=| 3 |
| 4 |
| A、6.3 | B、7.5 |
| C、8 | D、6.5 |
三角形的一个顶点A,可以用数对(5,6)表示,如果把这个三角形向上平移4格,这时点A用数对( )表示.
| A、(9,6) |
| B、(5,10) |
| C、(1,6) |
| D、(5,2) |
 如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB=
如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB=