题目内容
 △ABC在平面直角坐标系中的位置如图.
△ABC在平面直角坐标系中的位置如图.(1)将△ABC向上平移5个单位,画出平移后的△A1B1C1.
(2)画出△ABC关于y轴对称的△A2B2C2,并写出△A2B2C2各顶点的坐标A2
(3)求△ABC的面积.
考点:作图-轴对称变换,坐标与图形性质,作图-平移变换
专题:
分析:(1)利用平移的性质得出对应点位置,进而得出答案;
(2)利用关于y轴对称点的性质得出对应点位置,进而得出答案;
(3)利用△ABC面积=所在矩形面积减去周围三角形面积得出即可.
(2)利用关于y轴对称点的性质得出对应点位置,进而得出答案;
(3)利用△ABC面积=所在矩形面积减去周围三角形面积得出即可.
解答: 解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
A2 (0,-2),B2 (-2,-4),C2(-4,-1);
故答案为:(0,-2),(-2,-4),(-4,-1);
(3)△ABC的面积为:3×4-
×1×4-
×2×3-
×2×2=6.5.
 解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2B2C2,即为所求;
A2 (0,-2),B2 (-2,-4),C2(-4,-1);
故答案为:(0,-2),(-2,-4),(-4,-1);
(3)△ABC的面积为:3×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了平移变换以及轴对称变换和三角形面积求法,得出对应点位置是解题关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
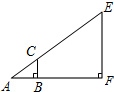 如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=
如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=| 3 |
| 4 |
| A、6.3 | B、7.5 |
| C、8 | D、6.5 |
已知⊙O的半径为10cm,如果圆心O到一条直线的距离为10cm,那么这条直线和这个圆的位置关系为( )
| A、相离 | B、相切 |
| C、相交 | D、无法确定 |
若
=
,则
=( )
| x+y |
| x |
| 5 |
| 3 |
| x-y |
| 2x |
| A、6 | ||
B、
| ||
C、
| ||
| D、不确定 |
下列变形中正确的是( )
| A、由3x-5=2x,得3x+2x=5 | ||
B、由-7x=3,得x=-
| ||
| C、由2(x-4)=4,得2x-1=4 | ||
| D、由-5y=0,得y=0 |
 如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E.已知GB=10cm,AG=2cm,DE=3cm,求EF的长.
如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E.已知GB=10cm,AG=2cm,DE=3cm,求EF的长.