题目内容
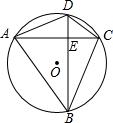 如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少?
如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少?考点:垂径定理,勾股定理
专题:计算题
分析:作OH⊥AB于H,OF⊥CD于F,连结OA、OC,如图,根据垂径定理得AH=
AB=4,DF=
CD=3,根据等腰三角形的性质得∠AOH=
∠AOB,∠DOF=
∠DOC,
而根据圆周角定理得到∠ACB=
∠AOB,∠DBC=
∠DOC,则∠AOH=∠ACB,∠DOF=∠DBC,再利用∠ACB+∠DBC=90°得到∠AOH+∠DOF=90°,于是根据等角的余角相等得∠OAH=∠DOF,则根据“AAS”可判断△AOH≌△ODF,所以OH=DF=3,然后在Rt△AOH中根据勾股定理计算OA.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而根据圆周角定理得到∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:作OH⊥AB于H,OF⊥CD于F,连结OA、OC,如图,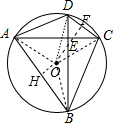
∵OH⊥AB,OF⊥CD,
∴AH=BH=
AB=4,DF=CF=
CD=3,
∴∠AOH=
∠AOB,∠DOF=
∠DOC,
∵∠ACB=
∠AOB,∠DBC=
∠DOC,
∴∠AOH=∠ACB,∠DOF=∠DBC,
∵AC⊥BD,
∴∠ACB+∠DBC=90°,
∴∠AOH+∠DOF=90°,
而∠AOH+∠OAH=90°,
∴∠OAH=∠DOF,
在△AOH和△ODF中,
,
∴△AOH≌△ODF(AAS),
∴OH=DF=3,
在Rt△AOH中,∵OH=3,AH=4,
∴OA=
=5,
即⊙O的半径是5.

∵OH⊥AB,OF⊥CD,
∴AH=BH=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOH=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOH=∠ACB,∠DOF=∠DBC,
∵AC⊥BD,
∴∠ACB+∠DBC=90°,
∴∠AOH+∠DOF=90°,
而∠AOH+∠OAH=90°,
∴∠OAH=∠DOF,
在△AOH和△ODF中,
|
∴△AOH≌△ODF(AAS),
∴OH=DF=3,
在Rt△AOH中,∵OH=3,AH=4,
∴OA=
| OH2+AH2 |
即⊙O的半径是5.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、圆周角定理和全等三角形的判定与性质.

练习册系列答案
相关题目
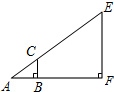 如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=
如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=| 3 |
| 4 |
| A、6.3 | B、7.5 |
| C、8 | D、6.5 |
三角形的一个顶点A,可以用数对(5,6)表示,如果把这个三角形向上平移4格,这时点A用数对( )表示.
| A、(9,6) |
| B、(5,10) |
| C、(1,6) |
| D、(5,2) |
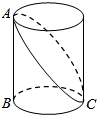 如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为
如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为