题目内容
 如图所示,阳光照射在一根因暴雨发生地陷而倾斜的电线杆AB上,已知AB的长为6m,此时顶点B到地面的距离BO为3m,某时刻身高为1.8m的小明在阳光下的影长为2.4m,求此时电线杆的影长为多少?
如图所示,阳光照射在一根因暴雨发生地陷而倾斜的电线杆AB上,已知AB的长为6m,此时顶点B到地面的距离BO为3m,某时刻身高为1.8m的小明在阳光下的影长为2.4m,求此时电线杆的影长为多少?考点:平行投影
专题:
分析:先根据勾股定理求出AD的长,然后根据相同时刻物高与影长成比例,求出DE的长,AD+DE就是电线杆的影长.
解答:解:在Rt△ADB中,由勾股定理得:
AD2+BD2=AB2,
即:AD2+32=62,
∴AD=3
,
∵相同时刻物高与影长成比例,
∴
=
,
即:
=
,
∴DE=4,
∴AE=AD+DE=3
+4.
∴电线杆的影长为3
+4(m).
AD2+BD2=AB2,
即:AD2+32=62,
∴AD=3
| 3 |
∵相同时刻物高与影长成比例,
∴
| BD |
| DE |
| 1.8 |
| 2.4 |
即:
| 3 |
| DE |
| 1.8 |
| 2.4 |
∴DE=4,
∴AE=AD+DE=3
| 3 |
∴电线杆的影长为3
| 3 |
点评:此题考查了平行投影,解题的关键是:根据相同时刻物高与影长成比例,求出DE的长.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
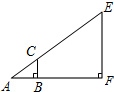 如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=
如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=| 3 |
| 4 |
| A、6.3 | B、7.5 |
| C、8 | D、6.5 |
已知⊙O的半径为10cm,如果圆心O到一条直线的距离为10cm,那么这条直线和这个圆的位置关系为( )
| A、相离 | B、相切 |
| C、相交 | D、无法确定 |
 如图,过△ABC顶点B,C分别作AB、AC的垂线BD、CD交于D,过C作CE⊥AD于E,求证:△ACE∽△ABC.
如图,过△ABC顶点B,C分别作AB、AC的垂线BD、CD交于D,过C作CE⊥AD于E,求证:△ACE∽△ABC. 如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB=
如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB=