题目内容
若一个四位数,其千位上的数字与十位上的数字相等,百位上的数字与个位上的数字相等,试说明这个四位数是101的倍数.
考点:列代数式
专题:
分析:设千位上的数字与十位上的数字为a,百位上的数字与个位上的数字为b,表示出这个四位数,再证明即可.
解答:解:∵千位上的数字与十位上的数字相等,百位上的数字与个位上的数字相等,
∴设千位上的数字与十位上的数字为a,百位上的数字与个位上的数字为b,
∴这个四位数为:1000a+100b+10a+b=1010a+101b=101(10a+b),
∵101(10a+b)是101的(10a+b)倍,
∴这个四位数是101的倍数.
∴设千位上的数字与十位上的数字为a,百位上的数字与个位上的数字为b,
∴这个四位数为:1000a+100b+10a+b=1010a+101b=101(10a+b),
∵101(10a+b)是101的(10a+b)倍,
∴这个四位数是101的倍数.
点评:本题考查了列代数式,设出各个数位上的数字,再表示出这个四位数是解题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
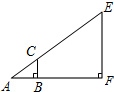 如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=
如图,利用标杆BC测量旗杆EF的高度,标杆BC长为1.2米,tanA=| 3 |
| 4 |
| A、6.3 | B、7.5 |
| C、8 | D、6.5 |
 如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB=
如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB=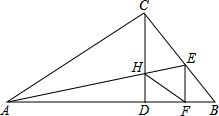 如图,在Rt△ABC中,∠ACB=90°,过C作AB的垂线CD交AB于D,过A作∠BAC的角平分线AE交BC于E,AE交CO于H,过E作EF⊥AB交AB于F,连接HF,求证:四边形CHFE为菱形.
如图,在Rt△ABC中,∠ACB=90°,过C作AB的垂线CD交AB于D,过A作∠BAC的角平分线AE交BC于E,AE交CO于H,过E作EF⊥AB交AB于F,连接HF,求证:四边形CHFE为菱形. 如图,∠AOC:∠COD:∠BOD=2:3:4,OE、OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.
如图,∠AOC:∠COD:∠BOD=2:3:4,OE、OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数. 如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E.已知GB=10cm,AG=2cm,DE=3cm,求EF的长.
如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E.已知GB=10cm,AG=2cm,DE=3cm,求EF的长.