题目内容
18. 如图,在矩形纸片ABCD中,CD=12,BC=15,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A1处,求AE的长度.
如图,在矩形纸片ABCD中,CD=12,BC=15,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A1处,求AE的长度.
分析 由在矩形纸片ABCD中,CD=12,BC=15,利用勾股定理即可求得BD的长,然后由折叠的性质,可得DA=DA1=BC=5,∠DA1E=∠DAE=90°,再设AE=x,利用勾股定理即可得方程:(12-x)2=x2+82,解此方程即可求得答案.
解答  解:∵在矩形纸片ABCD中,CD=12,BC=15,
解:∵在矩形纸片ABCD中,CD=12,BC=15,
由勾股定理求得:BD=3$\sqrt{41}$,
由折叠的性质可得:DA=DA1=BC=15,∠DA1E=∠DAE=90°,
设AE=x,则A1E=x,BE=12-x,BA1=3$\sqrt{41}$-15,
在Rt△EA1B中,(12-x)2=x2+(3$\sqrt{41}$-15)2,
解得:x=$\frac{15\sqrt{41}-75}{4}$,
即AE的长为$\frac{15\sqrt{41}-75}{4}$.
点评 此题考查了折叠的性质、矩形的性质以及勾股定理.注意掌握折叠前后图形的对应关系,掌握方程思想的应用是解此题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.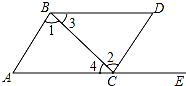 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠D=∠A | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠D=∠DCE |
9.抛物线y=x2+bx的对称轴经过点(2,0),那么关于x的方程x2+bx=5的两个根是( )
| A. | 0,4 | B. | 1,5 | C. | -1,5 | D. | 1,-5 |
10.直角三角形两个锐角∠A与∠B的函数关系是( )
| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
 如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,
如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,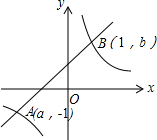 如图,已知反比例函数y=$\frac{2}{x}$与一次函数y=x+1的图象交于点A(a,-1)、B(1,b),则不等式$\frac{2}{x}$≥x+1的解集为x≤-2或0<x≤1.
如图,已知反比例函数y=$\frac{2}{x}$与一次函数y=x+1的图象交于点A(a,-1)、B(1,b),则不等式$\frac{2}{x}$≥x+1的解集为x≤-2或0<x≤1.