题目内容
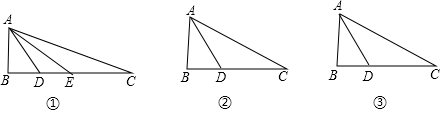
4.定义:若△ABC的一条角平分线AD满足AD2=BD•CD,那么我们把这条角平分线AD叫做这个三角形的角分中项线(1)如图①,△ABC中,点E为BC上一点,AD为△ABC的角平分线,且为△ABE的中线,且△ADE∽△CDA,求证AD为△ABC的角分中项线
(2)如图②,AD为△ABC的角分中项线
①求AB:BD
②若∠BAC=60°,BD=2,求S△ABD
③如图③,若△ABD为等腰三角形,且AD=$\sqrt{2}$,求AC的长.
分析 (1)由△ADE∽△CDA,推出$\frac{AD}{CD}$=$\frac{DE}{AD}$,即AD2=DE•DC,由BD=DE,即可推出AD2=BD•DC由此解决问题;
(2)①延长DB使得DE=DC.,作DM⊥AB于M,DN⊥AC于N.只要证明△ADB∽△EDA,推出∠DAB=∠E=∠CAD,推出△ACD∽△ECA,推出$\frac{AC}{EC}$=$\frac{CD}{AC}$,推出AC2=CD•CE=2CD2,即$\frac{AC}{CD}$=$\sqrt{2}$,由$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{BD}{DC}$=$\frac{\frac{1}{2}•AB•DM}{\frac{1}{2}•AC•DN}$,由DM=DN,可得$\frac{BD}{DC}$=$\frac{AB}{AC}$,推出$\frac{AB}{BD}$=$\frac{AC}{CD}$=$\sqrt{2}$;
②如图②-1中,作BH⊥AD于H.求出AD、BH即可解决问题;
③分两种情形a、如图③中,当AB=AD时,作AH⊥BD于H.b、如图④中,当DA=DB时,分别求解即可;
解答 (1)证明:如图1中,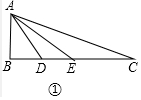
∵△ADE∽△CDA,
∴$\frac{AD}{CD}$=$\frac{DE}{AD}$,
∴AD2=DE•DC,
∵BD=DE,
∴AD2=BD•DC,
∴AD为△ABC的角分中项线.
解:(2)①延长DB使得DE=DC.,作DM⊥AB于M,DN⊥AC于N.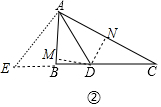
∵AD2=BD•DC=BD•DE,
∴$\frac{AD}{BD}$=$\frac{DE}{AD}$,
∵∠ADB=∠ADE,
∴△ADB∽△EDA,
∴∠DAB=∠E=∠CAD,∵∠C=∠C,
∴△ACD∽△ECA,
∴$\frac{AC}{EC}$=$\frac{CD}{AC}$,
∴AC2=CD•CE=2CD2,
∴$\frac{AC}{CD}$=$\sqrt{2}$,
∵$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{BD}{DC}$=$\frac{\frac{1}{2}•AB•DM}{\frac{1}{2}•AC•DN}$,
∵DM=DN,
∴$\frac{BD}{DC}$=$\frac{AB}{AC}$,
∴$\frac{AB}{BD}$=$\frac{AC}{CD}$=$\sqrt{2}$.
②如图②-1中,作BH⊥AD于H.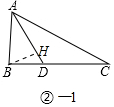
∵BD=2,AB=$\sqrt{2}$BD,
∴AB=2$\sqrt{2}$,
在Rt△ABH中,∵∠BAH=$\frac{1}{2}$∠BAC=30°,
∴BH=$\sqrt{2}$,AH=$\sqrt{6}$,
在Rt△BHD中,DH=$\sqrt{{2}^{2}-(\sqrt{2})^{2}}$=$\sqrt{2}$,
∴AD=$\sqrt{6}$+$\sqrt{2}$,
∴S△ABD=$\frac{1}{2}$•AD•BH=$\frac{1}{2}$•($\sqrt{6}$+$\sqrt{2}$)•$\sqrt{2}$=$\sqrt{3}$+1.
③如图③中,当AB=AD时,作AH⊥BD于H.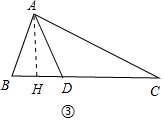
∵AB=AD=$\sqrt{2}$,AB=$\sqrt{2}$BD,
∴BD=1,
∵AD2=BD•DC,
∴CD=2,
在Rt△AHD中,AH=$\sqrt{A{D}^{2}-H{D}^{2}}$=$\frac{\sqrt{7}}{2}$,
在Rt△ACH中,AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\sqrt{(\frac{\sqrt{7}}{2})^{2}+(\frac{5}{2})^{2}}$=2$\sqrt{2}$.
如图④中,当DA=DB时,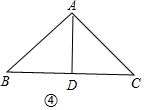
由题意AD=BD=$\sqrt{2}$,AB=2,
∵AD2=BD•DC,
∴DC=$\sqrt{2}$,
∵AB2=4,AD2+BD2=4,
∴AB2=BD2+AD2,
∴∠ADB=90°,
∴AD⊥BC,
∵BD=DC,
∴AC=AB=2.
点评 本题考查相似三角形综合题、勾股定理、相似三角形的判定和性质等知识,解题的关键是理解题意,学会添加常用辅助线,构造相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

| A. | a≥-5 | B. | a<1 | ||
| C. | -1<a<-2+$\frac{3\sqrt{5}}{2}$ | D. | -2-$\frac{3\sqrt{5}}{2}$<a<-5或1<a<-2+$\frac{3\sqrt{5}}{2}$ |
| A. | (-2,3) | B. | (2,3) | C. | (3,-2) | D. | (3,2) |
| A. | $\frac{720}{48+x}$-$\frac{720}{x}$=5 | B. | $\frac{720}{48}$+5=$\frac{720}{48+x}$ | C. | $\frac{720}{48}$-$\frac{720}{x}$=5 | D. | $\frac{720}{48}$-$\frac{720}{48+x}$=5 |
 如图所示,要在斜坡上A、B两点处测量与地面垂直的铁塔CD的高,由A、B两地测得塔顶C的仰角分别为60°和45°,AB的长为40米,斜坡与水平面成30°角,则铁塔CD的高是$\frac{40\sqrt{3}}{3}$米.
如图所示,要在斜坡上A、B两点处测量与地面垂直的铁塔CD的高,由A、B两地测得塔顶C的仰角分别为60°和45°,AB的长为40米,斜坡与水平面成30°角,则铁塔CD的高是$\frac{40\sqrt{3}}{3}$米. 如图,已知A(2,0),B(1,m2-4m+5).
如图,已知A(2,0),B(1,m2-4m+5).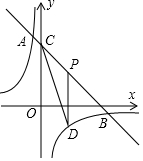 如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.
如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.