题目内容
2.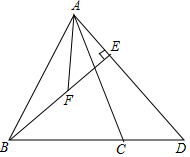 如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.(1)若BE=2$\sqrt{2}$,AE=$\sqrt{3}$,求AF的长;
(2)若∠BAC=∠DAF,求证:2AF=AD;
(3)请直接写出线段AD、BE、AE的数量关系.
分析 (1)在Rt△AEF中,利用勾股定理即可解决问题.
(2)如图,延长AF至M点,使AF=MF,连接BM,首先证明△AEF≌△MFB,再证明△ABM≌△ACD即可.
(3)结论:AD2=BE2+(AD-AE)2.在Rt△BED中,利用勾股定理即可证明.
解答 解:(1)∵BE的中点是F,BE=2$\sqrt{2}$,
∴EF=$\sqrt{2}$,
∵AE=$\sqrt{3}$,BE⊥AD,
∴AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{5}$,
(2)如图,延长AF至M点,使AF=MF,连接BM,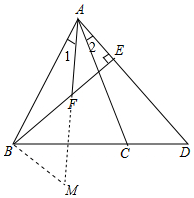
在△AEF和△MBF中,
$\left\{\begin{array}{l}{AF=FM}\\{∠AFE=∠BFM}\\{EF=BF}\end{array}\right.$
∴△AEF≌△MFB(SAS),
∴∠FAE=∠FMB,
∴AE∥MB,
∴∠EAB+∠ABM=180°,
又∵AB=AC,DB=DA,
∴∠ABC=∠ACB=∠BAD,
∴∠ACD=180°-∠ACB,∠ABM=180°-∠BAD,
∴∠ACD=∠ABM.又∵∠BAC=∠DAF,
∴∠1=∠2.
在△ABM和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠1=∠2}\\{∠ACD=∠ABM}\end{array}\right.$,
∴△ABM≌△ACD,
∴AM=AD,
∴2AF=AD
(3)结论:AD2=BE2+(AD-AE)2.
理由∵DB=DA,BE⊥AD,
∴BD2=BE2+DE2,
∴AD2=BE2+(AD-AE)2.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、勾股定理等知识,解题的关键是中线倍长一倍,构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
13.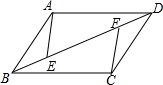 如图,AB=CD,AB∥DC,BE=DF,则图中的全等三角形有( )
如图,AB=CD,AB∥DC,BE=DF,则图中的全等三角形有( )
 如图,AB=CD,AB∥DC,BE=DF,则图中的全等三角形有( )
如图,AB=CD,AB∥DC,BE=DF,则图中的全等三角形有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
14.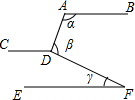 如图,直线AB∥CD∥EF,那么∠α+∠β-∠γ=( )
如图,直线AB∥CD∥EF,那么∠α+∠β-∠γ=( )
 如图,直线AB∥CD∥EF,那么∠α+∠β-∠γ=( )
如图,直线AB∥CD∥EF,那么∠α+∠β-∠γ=( )| A. | 60° | B. | 90° | C. | 180° | D. | 360° |
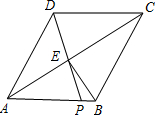 如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合).连接DP交对角线AC于E,连接BE.
如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合).连接DP交对角线AC于E,连接BE.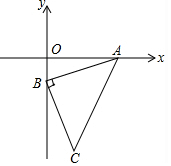 如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,-1),以AB为直角边在AB边的上方作等腰直角△ABE,则点E的坐标是(-1,2)或(2,3).
如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,-1),以AB为直角边在AB边的上方作等腰直角△ABE,则点E的坐标是(-1,2)或(2,3).