题目内容
17.解方程组:(1)$\left\{\begin{array}{l}{y=8-x}\\{2x-y=10}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x+y}{4}+\frac{x-y}{6}=1}\\{5(x+y)-3(x+2y)=2}\end{array}\right.$.
分析 (1)利用代入消元法直接将y=8-x代入第二个方程进行消元;
(2)先将方程组整理为一般形式,再利用加减法求解即可.
解答 解:(1)将y=8-x代入2x-y=10,
得2x-(8-x)=10,解得x=6,
将x=6代入y=8-x,得y=2,
所以原方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$;
(2)将方程组整理得$\left\{\begin{array}{l}{5x+y=12①}\\{2x-y=2②}\end{array}\right.$,
①+②,得7x=14,解得x=2.
将x=2代入②,得y=2
所以原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
点评 本题考查了二元一次方程组的解法.解二元一次方程组时,如果方程组中同一个未知数的系数成整数倍时,用加减消元法比较简便;如果方程组中有一个未知数的系数的绝对值是1或者常数项是0时,用代入消元法比较简便.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | 2x+y=0 | C. | x2+1=0 | D. | x2+y=3 |
12.下列方程组是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{2x-3y=3}\\{xy+x=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=2}\\{2y-k=8}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-y=0}\\{x+2y=9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{{x}^{2}+y=6}\\{3y-x=5}\end{array}\right.$ |
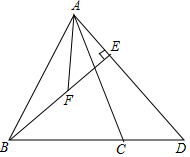 如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.