题目内容
11.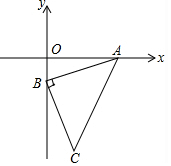 如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,-1),以AB为直角边在AB边的上方作等腰直角△ABE,则点E的坐标是(-1,2)或(2,3).
如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,-1),以AB为直角边在AB边的上方作等腰直角△ABE,则点E的坐标是(-1,2)或(2,3).
分析 如图,作EH⊥y轴于H,CF⊥y轴于F,E′G⊥OA于G.由△AOB≌△FBC≌△HBE≌△E′GA,可得CF=EH=AG=1,BH=BF=E′G=OA=3,由此即可解决问题.
解答 解:如图,作EH⊥y轴于H,CF⊥y轴于F,E′G⊥OA于G.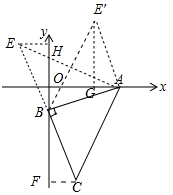
在△AOB和△FBC中,
$\left\{\begin{array}{l}{∠AOB=∠BFC}\\{∠ABO=∠BCF}\\{AB=BC}\end{array}\right.$,
∴△OAB≌△FBC,
∴CF=OB=1,BF=OA=3,
当B为直角顶点时,同理可得EH=1,BH=2,∴E(-1,2),
当A为直角顶点时,同理可得,AG=1,E′G=3,∴E′(2,3),
综上所述,点E坐标(-1,2)或(2,3).
故答案为(-1,2)或(2,3)
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质,坐标与图形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.一元二次方程x2-2x+4=0的根的情况是( )
| A. | 有一个实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
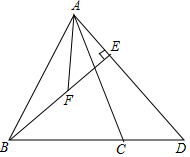 如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题: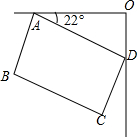 家用电冰箱在使用过程中能有效地散热是节电的有效途径之一.将一台家用电冰箱置于厨房的墙角,如图是它的俯视图,∠DAO=22°,冰箱的后背AD=110cm,AD平行于前沿BC,且与BC的距离为60cm,则从墙角O到前沿BC的距离约为(精确到1cm)( )
家用电冰箱在使用过程中能有效地散热是节电的有效途径之一.将一台家用电冰箱置于厨房的墙角,如图是它的俯视图,∠DAO=22°,冰箱的后背AD=110cm,AD平行于前沿BC,且与BC的距离为60cm,则从墙角O到前沿BC的距离约为(精确到1cm)( )