题目内容
12.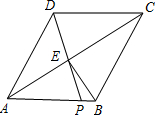 如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合).连接DP交对角线AC于E,连接BE.
如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合).连接DP交对角线AC于E,连接BE.(1)证明:∠APD=∠CBE;
(2)试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的$\frac{1}{4}$?请说明理由.
分析 (1)由四边形ABCD是菱形,即可证得∠CDE=∠APD,△CDE≌△CBE,继而证得结论;
(2)首先连接BE,由等高三角形的面积比等于对应底的比,可证得S△ADP=$\frac{1}{2}$S△ABD,继而证得结论.
解答 (1)证明:∵四边形ABCD是菱形,
∴CD=CB,∠DCE=∠BCE,AB∥CD,
∴∠CDE=∠APD,
在△CDE和△CBE中,
$\left\{\begin{array}{l}{CD=CB}\\{∠DCE=∠BCE}\\{CE=CE}\end{array}\right.$,
∴△CDE≌△CBE(SAS),
∴∠CBE=∠CDE,
∴∠APD=∠CBE; (2)P点运动到AB中点时,△ADP的面积等于菱形ABCD面积的$\frac{1}{4}$.
(2)P点运动到AB中点时,△ADP的面积等于菱形ABCD面积的$\frac{1}{4}$.
理由:连接BD,
∵P是AB的中点,
∴S△ADP=$\frac{1}{2}$S△ABD,
∵S△ABD=$\frac{1}{2}$S菱形ABCD,
∴S△ADP=$\frac{1}{4}$S菱形ABCD.
点评 此题考查了菱形的性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
20.某县12月份某一天的天气预报为气温-2~5℃,该天的温差为( )
| A. | -3℃ | B. | -7℃ | C. | 3℃ | D. | 7℃ |
7.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | 2x+y=0 | C. | x2+1=0 | D. | x2+y=3 |
4.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a5 | C. | a3÷a3=0 | D. | (a3)2=a9 |
1.一元二次方程x2-2x+4=0的根的情况是( )
| A. | 有一个实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
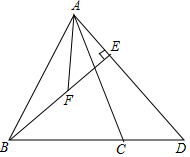 如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.