题目内容
已知P为△ABC的边AB上的点,且AP2+BP2+CP2-2AP-2BP-2CP+3=0,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
考点:因式分解的应用
专题:
分析:利用配方法得到(AP-1)2+(BP-1)2+(CP-1)2=0,易得AP=BP=CP=1,根据三角形一边上的中线等于这边的一半即可得到这个三角形为直角三角形进行判断.
解答:解:∵AP2+BP2+CP2-2AP-2BP-2CP+3=0,
∴(AP-1)2+(BP-1)2+(CP-1)2=0,
∴AP-1=0,BP-1=0,CP-1=0,
∴AP=BP=CP=1,
∴△ABC为直角三角形.
故选B.
∴(AP-1)2+(BP-1)2+(CP-1)2=0,
∴AP-1=0,BP-1=0,CP-1=0,
∴AP=BP=CP=1,
∴△ABC为直角三角形.
故选B.
点评:本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
相关题目
关于x,y的单项式ax2y,bxy2,
x2y,3xy2的和,合并同类项后结果是-6xy2,则a,b的值分别是( )
| 1 |
| 2 |
A、a=-
| ||
B、a=-
| ||
C、a=
| ||
D、a=
|
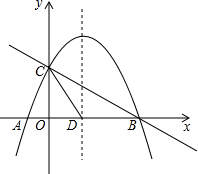 如图,直线y=-
如图,直线y=-