题目内容
7. 如图,EF∥AD,∠1=∠2,∠BAC=75°.
如图,EF∥AD,∠1=∠2,∠BAC=75°.(1)求证:AB∥DG;
(2)求∠AGD.
分析 (1)先根据两直线平行同位角相等可得∠2=∠3,然后根据等量代换可得∠1=∠3,然后根据内错角相等两直线平行可得AB∥DG;
(2)根据两直线平行同旁内角互补可得∠BAC+∠AGD=180°,进而可求∠AGD的度数
解答 (1)证明:∵EF∥AD,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥DG;
(2)解:∵AB∥DG,
∴∠BAC+∠AGD=180°.
∵∠BAC=75°,
∴∠AGD=105°.
点评 此题考查了平行线的判定与性质,解题的关键是熟记同旁内角互补,两直线平行.

练习册系列答案
相关题目
17.下列各式符合代数式书写规范的是( )
| A. | $5\frac{1}{4}{x^2}y$ | B. | yx3 | C. | ab+2 | D. | $\frac{2ab}{6}$ |
19.下面调查中,适合采用普查的是( )
| A. | 调查全国中学生心理健康现状 | B. | 调查你所在的班级同学的身高情况 | ||
| C. | 调查大东海食品合格情况 | D. | 调查交通法规普及情况 |
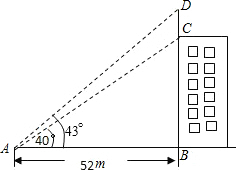 如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)
如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)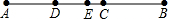 如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm.
如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm.