题目内容
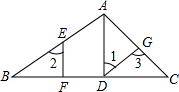
 如图,AF平分∠BAC,DF平分∠BDC,求证:∠AFD=
如图,AF平分∠BAC,DF平分∠BDC,求证:∠AFD=| 1 |
| 2 |
考点:三角形内角和定理,三角形的外角性质
专题:证明题
分析:延长AF交DH于E点,由三角形外角和定理和角平分线的性质,可以得到证明.
解答: 证明:延长AF交DH于E点.
证明:延长AF交DH于E点.
由三角形外角定理得:∠AFD=∠FDE+∠FED=∠FDE+∠H+∠HAE,
∵AF平分∠BAC,DF平分∠BDC,
∴∠AFD=
∠BDC+
∠BAC+∠H,
∵∠BGC=∠BDC+∠ACD=∠BDC+∠BAC+∠H,
∴
(∠BGC+∠H)=
(∠BDC+∠BAC+∠H+∠H)=
∠BDC+
∠BAC+∠H=∠AFD.
 证明:延长AF交DH于E点.
证明:延长AF交DH于E点.由三角形外角定理得:∠AFD=∠FDE+∠FED=∠FDE+∠H+∠HAE,
∵AF平分∠BAC,DF平分∠BDC,
∴∠AFD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BGC=∠BDC+∠ACD=∠BDC+∠BAC+∠H,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形外角和定理的简单应用,解答本题的关键在于利用角平分线的性质进行转化.

练习册系列答案
相关题目
 如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F. 在△ABC中,AC=4,AB=5,D是AC边上一点,E是AB边上一点,∠ADE=∠B.若CD=x,AE=y,求y与x的函数关系式.
在△ABC中,AC=4,AB=5,D是AC边上一点,E是AB边上一点,∠ADE=∠B.若CD=x,AE=y,求y与x的函数关系式.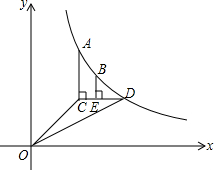 如图,已知函数y=
如图,已知函数y=
 如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为
如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为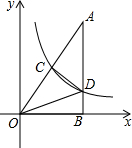 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=