题目内容
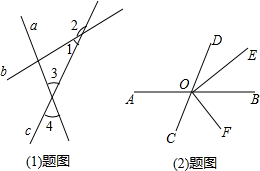 (1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.
(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF的度数.
考点:对顶角、邻补角,角平分线的定义
专题:
分析:(1)根据邻补角的和等于180°求出∠1的度数,然后求出∠3,再根据对顶角相等解答;
(2)利用角平分线及比例式求出角的关系,利用平角是180°,求出∠BOE=∠DOE=30°,OF平分∠COE得到∠EOF=75°,求出∠BOF=45°,根据邻补角的和等于180°求出∠AOF
(2)利用角平分线及比例式求出角的关系,利用平角是180°,求出∠BOE=∠DOE=30°,OF平分∠COE得到∠EOF=75°,求出∠BOF=45°,根据邻补角的和等于180°求出∠AOF
解答:
解:(1)如图,∵∠2=155°,
∴∠1=180°-∠2=180°-155°=25°,
∴∠3=2∠1=2×25°=50°,
∵∠3=∠4,(对顶角相等)
∴∠4=50°,
(2)∵∠AOD:∠BOE=4:1,
∴∠AOD=4∠BOE,
∵OE平分∠BOD,
∴∠D0E=∠EOB,
∴∠AOD+∠DOE+∠BOE=180°,
∴6∠BOE=180°,
∴∠BOE=∠DOE=30°,
∴∠COE=180°-30°=150°,
∵OF平分∠COE,
∴∠EOF=75°,
∴∠BOF=∠EOF-∠BOE=75°-30°=45°,
∠AOF=180°-45°=135°.

解:(1)如图,∵∠2=155°,
∴∠1=180°-∠2=180°-155°=25°,
∴∠3=2∠1=2×25°=50°,
∵∠3=∠4,(对顶角相等)
∴∠4=50°,
(2)∵∠AOD:∠BOE=4:1,
∴∠AOD=4∠BOE,
∵OE平分∠BOD,
∴∠D0E=∠EOB,
∴∠AOD+∠DOE+∠BOE=180°,
∴6∠BOE=180°,
∴∠BOE=∠DOE=30°,
∴∠COE=180°-30°=150°,
∵OF平分∠COE,
∴∠EOF=75°,
∴∠BOF=∠EOF-∠BOE=75°-30°=45°,
∠AOF=180°-45°=135°.
点评:本题考查了邻补角的定义,对顶角相等的性质,角平分线的定义,准确识图并熟记性质与概念是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
一组数据,6、4、a、3、2的平均数是5,这组数据的方差为( )
| A、8 | ||
| B、5 | ||
C、2
| ||
| D、3 |
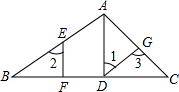 如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.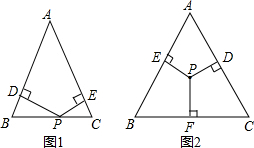 (1)如图1,在等腰△ABC中.AB=AC=a,面积是S,点P在BC上移动,过点P作PD⊥AB于点D,PE⊥AC于点E,那么点P到两腰的距离PD+PE等于什么?证明你的结论.
(1)如图1,在等腰△ABC中.AB=AC=a,面积是S,点P在BC上移动,过点P作PD⊥AB于点D,PE⊥AC于点E,那么点P到两腰的距离PD+PE等于什么?证明你的结论.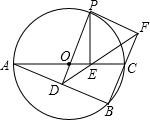 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF. 如图,已知函数y=
如图,已知函数y=