题目内容
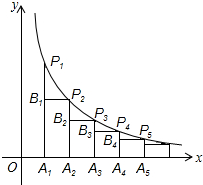 如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=
如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=| 1 |
| x |
考点:反比例函数系数k的几何意义
专题:压轴题,规律型
分析:根据反比例函数图象上点的坐标特征和三角形面积公式得到Rt△P1B1P2的面积=
×a×(
-
),Rt△P2B2P3的面积=
×a×(
-
),Rt△P3B3P4的面积=
×a×(
-
),由此得出△Pn-1Bn-1Pn的面积=
×a×[
-
],化简即可.
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 3a |
| 1 |
| 2 |
| 1 |
| 3a |
| 1 |
| 4a |
| 1 |
| 2 |
| 1 |
| (n-1)a |
| 1 |
| na |
解答:解:设OA1=A1A2=A2A3=…=An-2An-1=a,
∵x=a时,y=
,∴P1的坐标为(a,
),
∵x=2a时,y=2×
,∴P2的坐标为(2a,
),
∴Rt△P1B1P2的面积=
×a×(
-
),
Rt△P2B2P3的面积=
×a×(
-
),
Rt△P3B3P4的面积=
×a×(
-
),
…,
∴△Pn-1Bn-1Pn的面积=
×a×[
-
]=
×1×(
-
)=
.
故答案为:
.
∵x=a时,y=
| 1 |
| a |
| 1 |
| a |
∵x=2a时,y=2×
| 1 |
| a |
| 1 |
| 2a |
∴Rt△P1B1P2的面积=
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2a |
Rt△P2B2P3的面积=
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 3a |
Rt△P3B3P4的面积=
| 1 |
| 2 |
| 1 |
| 3a |
| 1 |
| 4a |
…,
∴△Pn-1Bn-1Pn的面积=
| 1 |
| 2 |
| 1 |
| (n-1)a |
| 1 |
| na |
| 1 |
| 2 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 2n(n-1) |
故答案为:
| 1 |
| 2n(n-1) |
点评:本题考查了反比例函数图象上点的坐标特征和三角形面积公式,有一定难度.

练习册系列答案
相关题目
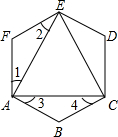 如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数.
如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数.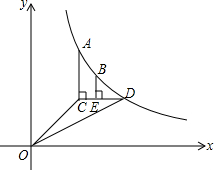 如图,已知函数y=
如图,已知函数y=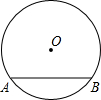 如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为
如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表: