题目内容
5. 如图,AD平分∠BAC,BD平分∠FBC,CD⊥BE于点O,求证:BC=EC.
如图,AD平分∠BAC,BD平分∠FBC,CD⊥BE于点O,求证:BC=EC.
分析 作DM⊥BF于M,DN⊥BC于N,DP⊥AC于P,利用角平分线的性质可得DM=DN=DP,证得△BOC≌△EOC,由全等三角形的性质可得BC=EC.
解答  证明:作DM⊥BF于M,DN⊥BC于N,DP⊥AC于P,
证明:作DM⊥BF于M,DN⊥BC于N,DP⊥AC于P,
∵AD平分∠BAC,
∴DM=DP,
同理可证:DM=DN,
∴DP=DN,
则CD平分∠BCE,
∴∠BCD=∠ECD,
在△CBO和△CEO中,
$\left\{\begin{array}{l}{∠BCD=∠ECD}\\{CO=CO}\\{∠COB=∠COE=90°}\end{array}\right.$,
∴△BOC≌△EOC(ASA),
∴BC=EC.
点评 本题主要考查了角平分线的性质和等腰三角形的性质,作出适当的辅助线是解答此题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
15.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形,正三角形,等腰梯形和菱形四种图形,你认为符合条件的是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 等腰梯形 | D. | 菱形 |
16.一个三角形的两边a,b的长分别为3,5,则第三边c的取值范围是( )
| A. | 3<c<5 | B. | 2<c<8 | C. | 3≤c≤5 | D. | 2≤c≤8 |
13.|-25|的平方根为( )
| A. | 5 | B. | -5 | C. | 25 | D. | 5或-5 |
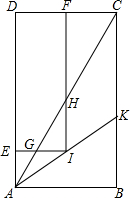 如图,已知矩形ABCD中,点I在∠CAB的平分线AK上运动,过I作IE⊥AD,IF⊥CD,垂足分别为E,F,IE、IF分别交AC于点G、H.
如图,已知矩形ABCD中,点I在∠CAB的平分线AK上运动,过I作IE⊥AD,IF⊥CD,垂足分别为E,F,IE、IF分别交AC于点G、H.