题目内容
11.当x<-$\frac{1}{2}$时,分式$\frac{-2}{2x+1}$的值为正.当整数x=4或2或8或-2时,分式$\frac{5}{x-3}$的值为整数.分析 直接利用分式的分子符号确定其分母的符号,进而得出答案,再利用整数的定义得出x的值.
解答 解:当2x+1<0时,分式$\frac{-2}{2x+1}$的值为正.
解得:x<-$\frac{1}{2}$;
当整数x-3=1或x-3=-1或x-3=5或x-3=-5时,分式$\frac{5}{x-3}$的值为整数,
解得:x=4或2或8或-2.
故答案为:<-$\frac{1}{2}$;=4或2或8或-2.
点评 此题主要考查了分式的值,正确分类讨论求出x的值是解题关键.

练习册系列答案
相关题目
16.已知点P1(x1,y1)和点P2(x2,y2)是正比例函数y=-x+1图象上的两点,则下列判断正确的是( )
| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1>y2 | D. | 当x1<x2时,y1<y2 |
3.若整数x能使分式$\frac{3x-3}{{x}^{2}-1}$的值是整数,则符合条件的x的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )| A. | $\frac{12}{5}$ | B. | $\frac{14}{5}$ | C. | $\frac{16}{5}$ | D. | 4 |
1.分式$\frac{x}{x-1}$+$\frac{1}{1-x}$可化简为( )
| A. | $\frac{x+1}{x-1}$ | B. | 1 | C. | -1 | D. | $\frac{x+1}{1-x}$ |
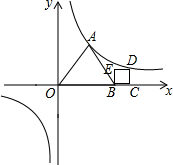 已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$).
已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$). 一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?)
一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?)