题目内容
6.已知点P(1,3),将线段OP绕原点O按顺时针方向旋转90°得到线段OP′,则点P′的坐标是( )| A. | (-1,3) | B. | (1,-3) | C. | (3,-1) | D. | (3,1) |
分析 先根据旋转的性质,得到OP=OP',∠POP'=90°,再过P作PD⊥x轴于D,过P'作P'E⊥x轴于E,得到△POD≌△OP'E(AAS),即可得到P'E=OD=1,OE=PD=3,进而得出P'(3,-1).
解答  解:如图所示,由旋转可得OP=OP',∠POP'=90°,
解:如图所示,由旋转可得OP=OP',∠POP'=90°,
过P作PD⊥x轴于D,过P'作P'E⊥x轴于E,则
∠PDO=∠OEP'=90°,∠P+∠POD=∠P'OE+∠POD=90°,
∴∠P=∠P'OE,
在△POD和△OP'E中,
$\left\{\begin{array}{l}{∠PDO=∠OEP'}\\{∠P=∠P'OE}\\{OP=OP'}\end{array}\right.$,
∴△POD≌△OP'E(AAS),
∴P'E=OD=1,OE=PD=3,
∴P'(3,-1),
故选:C.
点评 此题考查了坐标与图形变化,旋转的性质以及全等三角形的判定与性质.解题时注意掌握旋转前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
15.下列调查中,调查方式选择错误的是( )
| A. | 为了解全市中学生的课外阅读情况,选择全面调查 | |
| B. | 旅客上飞机前的安检,选择全面调查 | |
| C. | 为了了解《人民的名义》的收视率,选择抽样调查 | |
| D. | 为保证“神舟十一号”载人飞船的成功发射,对其零部件的检查,选择全面调查 |
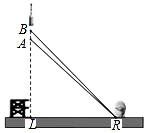 2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°
2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°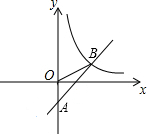 如图,在平面直角坐标系中,直线AB与y轴相交于点A(0,-2),与反比例函数在第一象限内的图象相交于点B(m,2),△AOB的面积为4.
如图,在平面直角坐标系中,直线AB与y轴相交于点A(0,-2),与反比例函数在第一象限内的图象相交于点B(m,2),△AOB的面积为4.