题目内容
9.已知α、β是方程x2-11x+22=0的二根,求作以α+β、$\frac{β}{α}$+$\frac{α}{β}$为根的一元二次方程.分析 先利用根与系数的关系得到α+β=11,αβ=22,再计算出$\frac{β}{α}$+$\frac{α}{β}$=$\frac{7}{11}$,接着计算出α+β+$\frac{β}{α}$+$\frac{α}{β}$和(α+β)($\frac{β}{α}$+$\frac{α}{β}$)的值,然后利用根与系数的关系写出满足条件的方程.
解答 解:根据题意得α+β=11,αβ=22,
所以$\frac{β}{α}$+$\frac{α}{β}$=$\frac{{α}^{2}+{β}^{2}}{αβ}$=$\frac{(α+β)^{2}-2αβ}{αβ}$=$\frac{1{1}^{2}-2×22}{22}$=$\frac{7}{11}$,
所以α+β+$\frac{β}{α}$+$\frac{α}{β}$=11+$\frac{7}{11}$=$\frac{128}{11}$,(α+β)($\frac{β}{α}$+$\frac{α}{β}$)=11×$\frac{7}{11}$=7,
所以以α+β、$\frac{β}{α}$+$\frac{α}{β}$为根的一元二次方程为x2-$\frac{128}{11}$x+7=0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
19. 如图,在△ABC和△DEF中,AB=DE,AB∥DE,添加下列条件仍无法证明△ABC≌△DEF的是( )
如图,在△ABC和△DEF中,AB=DE,AB∥DE,添加下列条件仍无法证明△ABC≌△DEF的是( )
 如图,在△ABC和△DEF中,AB=DE,AB∥DE,添加下列条件仍无法证明△ABC≌△DEF的是( )
如图,在△ABC和△DEF中,AB=DE,AB∥DE,添加下列条件仍无法证明△ABC≌△DEF的是( )| A. | AC∥DF | B. | ∠A=∠D | C. | AC=DF | D. | BE=CF |
20.若关于x的方程mx2-(2m-1)x+m=0有实数根,则( )
| A. | m≥$-\frac{1}{4}$ | B. | m≥$-\frac{1}{4}$且m≠0 | C. | m≤$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$且m≠0 |
18.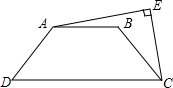 在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于( )
在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于( )
 在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于( )
在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于( )| A. | 84 | B. | 80 | C. | 75 | D. | 64 |
4.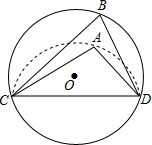 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )| A. | 100° | B. | 80° | C. | 60° | D. | 50° |
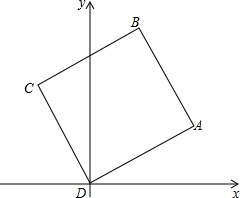 正方形ABCD如图放置,D与原点重合,C在第二象限,A点坐标为(8,4).
正方形ABCD如图放置,D与原点重合,C在第二象限,A点坐标为(8,4).