题目内容
18.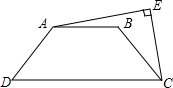 在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于( )
在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于( )| A. | 84 | B. | 80 | C. | 75 | D. | 64 |
分析 如图,连接AC,过点A作AF⊥CD于点F,过点B作BG⊥CD于点G,构建直角△AFC和直角△BGC,结合勾股定理求得AE2的值.
解答 解: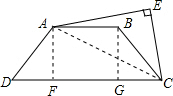 如图,连接AC,过点A作AF⊥CD于点F,过点B作BG⊥CD于点G,则AF=BG,AB=FG=6,DF=CG=4.
如图,连接AC,过点A作AF⊥CD于点F,过点B作BG⊥CD于点G,则AF=BG,AB=FG=6,DF=CG=4.
在直角△AFC中,AC2=AF2+FC2=AF2+102=AF2+100,
在直角△BGC中,BC2=BG2+GC2=AF2+42=AF2+16,
又∵CE=CB,∠AEC=90°,
∴AE2=AC2-EC2=AF2+100-(AF2+16)=84,即AE2=84.
故选A
点评 本题考查了等腰梯形的性质,勾股定理的应用.解题的关键是作出辅助线,构建直角三角形,利用勾股定理来求AE2的值.

练习册系列答案
相关题目
8.同一平面内的三条直线满足a⊥b,b⊥c,则下列式子成立的是( )
| A. | a∥c | B. | a∥b | C. | b∥c | D. | a⊥c |
12.一个整式减去a2-b2等于a2+b2,则这个整式为( )
| A. | 2b2 | B. | 2a2 | C. | -2b2 | D. | -2a2 |
13.(-2)3的底数是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.