题目内容
5.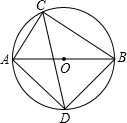 如图,圆O的直径AB为4,点C在圆O上,∠ACB的平分线交圆O于点D,连接AD、BD,则AD的长等于( )
如图,圆O的直径AB为4,点C在圆O上,∠ACB的平分线交圆O于点D,连接AD、BD,则AD的长等于( )| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 连接OD.利用直径所对的圆周角是直角及勾股定理求出AB的长,再根据角平分线的性质求出∠ACD=45°;然后根据同弧所对的圆周角是圆心角的一半求得∠AOD=90°;最后根据在等腰直角三角形AOD中利用勾股定理求AD的长度
解答 解:连接OD.
∴∠ACB=∠ADB=90°,
∵∠ACB的平分线交⊙O于D,
∴D点为半圆AB的中点,
∴△ABD为等腰直角三角形,
∴AD=AB÷$\sqrt{2}$=2$\sqrt{2}$cm.
故选 C.
点评 本题考查了圆周角定理、等腰直角三角形的判定与性质.解答该题时,通过作辅助线OD构造等腰直角三角形AOD,利用其性质求得AD的长度的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列汽车标志可以看作是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.一元二次方程x2-mx+2m=0有两个相等的实数根,则m等于( )
| A. | 0或8 | B. | 0 | C. | 8 | D. | 2 |
14. 如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y的值是( )
如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y的值是( )
 如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y的值是( )
如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y的值是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
15.已知两个相似三角形的相似比为1:4,则它们的周长比为( )
| A. | 1:4 | B. | 4:1 | C. | 1:2 | D. | 1:16 |